A Brief History of Time

1-Page Summary

Science has profound implications for philosophy and everyday life because science describes and predicts how the universe works. To make the discoveries and implications of modern science more accessible to everyone, renowned physicist Stephen Hawking described the principles of modern physics for a general audience in A Brief History of Time.

In this guide, we’ll present Hawking’s exposition of modern physics through the lens of five big questions that the book answers: Is reality relative or absolute? Is the future predetermined? How did the universe begin? What is the nature of a black hole? And can you build a time machine?

Question 1: Is Reality Relative or Absolute?

Science is founded on the assumption that reality works the same for everyone: If two scientists conduct exactly the same experiment, they should get the same results. Ironically, this principle has driven scientists to the conclusion that many things—including motion, position, time, and weight—are relative to the observer.

Motion Is Relative

Hawking explains that motion is relative to the observer, because there is no absolute reference frame.

To illustrate this concept, imagine you’re sitting in a boat on a body of water. Looking into the water, you see a fish swim by. Relative to your frame of reference, the fish is moving at a certain speed. But an observer on land might disagree. Let’s say the body of water is a river, and the fish is holding a constant position, relative to the river bottom, while your boat drifts by. So is the fish moving or staying in the same place? In an absolute sense, we can’t tell. Relative to your boat, the fish is moving. Relative to the earth, the fish is stationary. But of course the earth is also moving, relative to the sun, so the fish is moving relative to the sun. And the sun is moving, relative to the galaxy, and so on.

(Shortform note: One familiar scenario where the relativity of speed becomes important is driving a car. To avoid collisions, you have to keep track of the motion of other cars relative to your own. You also have to keep track of your speed relative to the road, since posted speed limits are implicitly specified relative to the road. To maintain a constant following distance behind another car, you have to adjust your speed to be zero relative to the other car.)

Time Is Relative

In the same way that the motion of objects is relative to the observer, Hawking argues that different observers may measure time differently. Hawking explains that, in particular, time appears to slow down for entities that are moving very fast. This is because of the relationship between time, speed, and distance, and the fact that everyone who accurately measures the speed of light gets the same result. He notes that this is true regardless of their particular reference frame, because the laws of physics are consistent for all observers.

For example, imagine two kids playing laser tag on a starship that is traveling at the speed of light. As they fire pulses of light back and forth, from opposite sides of the ship, an observer on the ship measures the distance that the light travels and finds it equal to the width of the ship. But if you’re outside the ship, you would see the light traveling a greater distance. Specifically, the distance would be the hypotenuse of a right triangle, with one leg equal to the width of the ship, and the other equal to the distance the ship traveled while the light was moving across it. Since you perceive the light traveling a greater distance (at the same speed) than the people on the starship, you must also perceive more time elapsing during the event than they do.

Relativity

When time progresses at a different rate for one person than another, scientists call this “time dilation.” As Hawking points out, Albert Einstein developed his theories of relativity as a mathematical model for predicting the motion of objects, even at speeds where time dilation becomes significant. (Earlier theories of motion didn’t account for time dilation.)

As Hawking recounts, Einstein introduced his theory of relativity in two phases: first, special relativity and then general relativity. Let’s discuss each of these theories in turn.

(Shortform note: “Special relativity” is “special” because it only works in situations where there is no gravity or acceleration. Physics problems with no gravity or acceleration are simpler, and constitute a “special case,” where a relatively simple theory of relativity can be applied.)

As Hawking recounts, when Einstein developed his theory of special relativity he ignored gravity and acceleration to make the mathematical derivation simpler. This allowed him to publish his theory quickly and gain support for it. Then he developed his theory of general relativity as a more generalized version of the theory, which could account for gravity and acceleration as well.

Hawking notes that the key idea that allowed Einstein to complete the theory of general relativity was his realization that gravity could be viewed as the curvature of space itself. In other words, general relativity is based on the principle that mass actually causes space to warp, such that the shortest distance between two points is an arc segment, rather than a straight line.

Testing General Relativity

Initially, Einstein’s theory of general relativity was somewhat controversial, and so it was subjected to even more testing than most theories. So far, the test results support the theory.

Since general relativity is a theory of motion and gravity, most tests of the theory involve using it to predict the motion of astronomical bodies like planets, stars, and black holes (we’ll discuss black holes more in Question 5), and comparing these predictions with observations.

The first widely-publicized test of general relativity came in 1915, when Einstein used his theory to predict the orbit of the planet Mercury. He predicted that the orbit would be slightly different from what Newtonian Mechanics predicted—and he was right.

More recently, general relativity has been tested using LIGO, the Laser Interferometer Gravitational Observatory, which detects gravity waves. General relativity predicts that since gravity is the curvature of space, massive objects moving through space should create ripples in spacetime. These ripples are called gravity waves. The heavier the objects and the faster they move, the more gravity waves they produce. Researchers at LIGO have observed gravity waves from colliding black holes and have found them to be consistent with what general relativity predicts.

Mass Is Relative

We’ve discussed how time is relative to speed (if you’re moving very fast, relative to someone else, you perceive less time passing than they do), and we’ve discussed how Einstein developed his theories of relativity to model this phenomenon. As Hawking explains, it turns out that the theories of relativity also imply that mass is relative to speed and time is relative to gravity. Specifically, Hawking explains that, as an object accelerates to speeds closer and closer to the speed of light, its mass increases, such that it can never actually reach the speed of light.

Alternative Explanation

Experimental data from particle accelerators conclusively demonstrates that, as the speed of a particle increases, the energy required to further increase its speed also increases, just as the theory of relativity predicts.

However, some scientists have argued that this is not because the mass of the particle increases. Instead, it's because the forces used to accelerate the particle (typically electromagnetic forces) travel at the speed of light, and so the force they apply to the particle decreases as its speed approaches their own speed.

To illustrate this principle, imagine a sailboat. When you first hoist the sails and catch the wind, the force of the wind against the sails is strong, and the boat accelerates. However, as the speed of the boat starts to approach the speed of the wind, the wind no longer pushes on the sails as hard, and the acceleration of the boat tapers off. If the sailboat could go the same speed as the wind, then the wind would no longer apply any force to the sails.

Question 2: Is the Future Predetermined?

As we have seen, scientific theories allow us to model the behavior of objects and predict their behavior. Hawking points out that if you could formulate a unified theory of physics and if you knew the exact state of the entire universe at any point in time, you could use that theory to predict the state of the universe at any other time.

This would make human free will an illusion, since you could calculate everyone’s future actions. Hawking refers to this as “scientific determinism.” However, he also discusses three limitations of scientific determinism:

1. There Is No Unifying Theory (Yet)

Hawking points out that general relativity works well for modeling the motion of stars and other macroscopic objects (objects big enough to see without a microscope), but relativity does not accurately model the behavior of subatomic particles. Instead, subatomic particles exhibit a variety of behaviors that can only be modeled using quantum mechanics.

As Hawking explains, quantum mechanics accurately models subatomic particles, but quantum mechanics doesn’t allow for modeling gravitational interactions or macroscopic objects. This is because the mass of subatomic particles is too small for scientists to measure their gravitational interactions. And you can’t simply add more particles to make them easier to measure, because, according to Hawking, the calculations quickly become prohibitively complex as the number of particles increases.

(Shortform note: Astrophysicist Paul Sutter offers a slightly different explanation for the incompatibility of quantum mechanics and gravity. He explains that, when calculating particle interactions in quantum mechanics, scientists assume that space is Euclidean (not curved) and is not affected by the particles. But general relativity assumes that the presence of mass causes space to warp, creating gravity. If you try to incorporate curved space into quantum mechanics, that adds a whole new dimension of complexity, making the math problem insoluble.)

Is Thermodynamics the Unifying Theory?

Hawking asserts that no one has yet come up with a complete theory that incorporates both quantum mechanics and general relativity. However, in 2011, Pharis E. Williams published a book on “Dynamic Theory,” which allegedly provides a simple yet powerful way to unify quantum mechanics and general relativity.

The essence of Williams’s approach was to generalize the first and second laws of thermodynamics in five dimensions: three dimensions of space, one of time, and one of mass. Williams shows how, if you make certain simplifying assumptions, this set of equations reduces to the equations of quantum mechanics, while if you make different simplifying assumptions, they reduce to the equations of general relativity. If you don’t assume either special case and keep all the terms in Williams’s model, then it appears to provide a unifying theory that’s universally applicable. However, Williams’s theory has yet to be rigorously tested.

2. Quantum Mechanics Is Not Deterministic

Hawking explains that quantum mechanics imposes another limitation of scientific determinism because solutions to quantum mechanics problems are probabilistic, not deterministic. In other words, if you model the motion of a particle with quantum mechanics, you get a probability map, showing you where the particle is most likely to go, and where it is less likely to go.

(Shortform note: While the probabilistic nature of quantum theory limits its predictive power, a side benefit is that the study of quantum mechanics has advanced the science of probability and statistics. Mathematicians are just beginning to explore the possibility of adapting methods from quantum mechanics to general statistical modeling, but this is already creating new mathematical tools for statistical analysis.)

3. Quantum Uncertainty Restricts Measurements

We’ve discussed how quantum mechanics limits your ability to predict the future because it’s probabilistic instead of deterministic, but quantum mechanics also limits your ability to measure the present state of the universe because of the uncertainty principle.

As Hawking explains, the uncertainty principle states there is always at least a certain amount of uncertainty in your measurement of the position and velocity of a particle. And uncertainty about the present creates greater uncertainty about the future, because to predict where a particle is likely to go in the future, you need to know where it was at some point in the past or present, and how fast it was going at the time.

To understand how the uncertainty principle works, you need to understand a few things about quantum mechanics. For one thing, as Hawking notes, the basic premise of quantum mechanics is that certain quantities, like energy, are “quantized,” meaning that they can only have certain values, or be incremented by at least a certain minimum value.

(Shortform note: This minimum unit is called a “quantum” of energy, which is where “quantum mechanics” gets its name.)

For another thing, you can only see something if it is reflecting (or otherwise emitting) light. If there’s no light, you won’t be able to see it. But bouncing light off of a subatomic particle will change its velocity. And since energy is quantized, you have to disturb a particle by at least a certain amount to measure it. Thus, there will always be at least a certain amount of uncertainty in your measurement.

Measurement Error Versus Quantum Uncertainty

It is important to distinguish between ordinary measurement uncertainty and quantum uncertainty.

In real life, every measuring device has limited precision. For example, if you measure the length of something with a ruler, your measurement is only as accurate as the marks on the ruler. In general, the better your measuring tools, the less uncertainty there will be in your measurement.

But, the uncertainty principle imposes additional limits on your ability to measure the position and velocity of a particle. So even in the hypothetical case where you had perfect measuring tools, there would still be uncertainty in your measurement, because the light that allows you (or your instruments) to see the particle changes its velocity as you’re trying to measure it.

Question 3: How Did the Universe Begin?

Hawking points out that the origins of the universe have profound philosophical implications. He contrasts the Judeo-Christian belief that God created the universe at some point in the past with the atheistic view that many scientists held in the nineteenth century, namely that the universe was infinite and had always existed.

Hawking recounts that in the twentieth century, new scientific discoveries challenged the theory that the universe had always existed. Based on these discoveries, the “big bang” theory replaced the static universe model. The big bang theory posits that the universe is expanding outward from a point where it came into existence at a finite time in the past.

Let’s take a look at the discoveries that provided evidence for the big bang, and then consider its implications.

Evidence for the Big Bang

The primary piece of evidence that led to the development of the big bang was the discovery that the universe is expanding, which was supported by both theory and observation.

Hawking recounts how, in the 1920s, astronomer Edwin Hubble measured the distance to a number of galaxies and found that they were all moving away from our own. Furthermore, the galaxies that were farther away were moving away faster. This provided direct observational evidence that the universe is expanding.

Hawking also points out that, in hindsight, Hubble’s discovery that the universe is expanding could have been predicted based on general relativity. Einstein recognized this when he first developed the theory of general relativity. But at the time, Hawking explains, the static universe model was so entrenched in the scientific community that Einstein introduced a hypothetical constant into his equations to cancel out the expansion. He called this fudge factor the “cosmological constant.” Hawking recounts that after Hubble’s observations were publicized, Einstein admitted publicly that introducing this hypothetical constant was a mistake.

(Shortform note: Ironically, scientists have recently reintroduced Einstein’s cosmological constant into the theory of general relativity, but with a different value, so that it accelerates the expansion of the universe instead of canceling it out. They’ve done this to explain new observations. Specifically, new measurements indicate that after the big bang, gravity began to slow down the expansion of the universe for a while, but now the expansion rate is speeding up again.)

The Cosmic Microwave Background

As Hawking explains, there was another discovery that helped to establish the big bang theory. Specifically, the big bang theory implies that there was a period of time where the early universe was small, hot, and dense. According to Hawking, physicists calculated that at this stage in its development, the universe would have given off a uniform glow, which should still be detectable in the microwave part of the electromagnetic spectrum.

He also tells how, in the 1960s, astronomers Arno Penzias and Robert Wilson were trying out a very sensitive microwave antenna when they discovered faint, uniform microwave radiation that seemed to come from every direction. This radiation was later dubbed the “cosmic microwave background,” and was exactly what theories predicted the big bang would have produced.

(Shortform note: About the same time that Penzias and Wilson discovered cosmic microwave background radiation, astronomers also discovered a similar background signal in the radio portion of the spectrum. Unlike the microwave background, the radio background is not predicted or explained by the big bang model. Nevertheless, recent measurements have confirmed its existence and revived interest in it. Scientists have not yet determined what causes it.)

Implications of the Big Bang

Hawking had two concerns about the big bang, at least as it was modeled using general relativity.

His first concern was the fine-tuning problem. According to mathematical models, certain physical parameters of the early universe, such as its initial rate of expansion, had to be specified very precisely. If they had been even slightly different, the universe would not have developed in a way that could support human life. To Hawking, this indicated a problem, because it seemed to imply that human life was highly improbable, and yet we observe that human life exists.

His second concern was the singularity. Hawking himself first became famous in the physics community for proving mathematically that, based on the equations of general relativity, the big bang started at a “singularity,” a point where matter, space, and time, are confined to an infinitely small space with infinitely high density. Matter, space, and even time itself came into being at this infinitesimal point, and the universe expanded outward from there. However, reflecting later on his own theoretical proofs, Hawking came to believe that they imply the theory of general relativity is incomplete, not that the universe actually did begin at a singularity. He saw the infinite density of the universe at the singularity as a red flag, because physical quantities are never infinite in real life.

Hawking suggests that a quantum theory of gravity would resolve both his concerns. He expects that it would eliminate the singularity and provide an explanation for the initial parameters of the universe.

(Shortform note: However, a workable theory of quantum gravity has not yet been developed, so Hawking’s expectations have not yet been proven.)

Did Hawking Prove the Existence of God?

Some Christians have used the big bang theory and Hawking’s proof that time had a beginning as an argument for the existence of God and the divine creation of the universe.

Physicists sometimes define time as the dimension in which cause and effect take place, such that causes always come before the effects that they produce. If time itself came into being at some point (an effect), then there must be a cause that exists independent of the space-time of our universe to bring it into existence (cause the effect), because there is no time prior to that for a cause within our universe to trigger the big bang. Anything independent from spacetime would, by definition, be supernatural.

Advocates of this argument also pick up on the fine-tuning of the initial conditions of the universe as evidence that God designed the universe to support human life, rather than seeing the fine-tuning as a problem, as Hawking does.

Question 4: What Is a Black Hole?

Hawking explains that a “black hole” is an object with such strong gravity that its gravity can trap light. And if light can’t escape from a black hole, then nothing can, since general relativity implies that nothing can travel faster than light. He points out that the closer you get to an object, the more its gravity pulls on you. The threshold where light gets trapped forms an imaginary surface around the black hole called the “event horizon.”

(Shortform note: It’s called an “event horizon” because you can’t observe events that happen beyond it. Light from an event has to reach you for you to observe the event, and light that passes inside the event horizon can’t reach you because it can’t escape from the gravity of the black hole.)

Hawking explains that most black holes form from collapsing stars. Normally pressure from nuclear fusion counterbalances a star’s gravity, but if a sufficiently massive star runs out of nuclear fuel, it can undergo runaway gravitational collapse, producing a black hole.

(Shortform note: Nuclear fusion is when the nuclei of two atoms merge to form a new, heavier atomic nucleus. When light atoms like hydrogen and helium combine, this process releases energy. But, for atoms heavier than iron, nuclear fusion actually consumes energy, so a star runs out of energy when all of its lighter elements have been fused into heavier ones.)

(Shortform note: Since the publication of the book, astronomers have identified many other black holes or likely black-hole candidates.)

Hawking Radiation

Nothing can escape from inside the event horizon of a black hole, but radiation that’s produced just outside the event horizon can escape—and if it originates just outside the event horizon, it would appear to be coming from the black hole itself.

According to Hawking, the theory of quantum mechanics predicts that “empty” space is actually full of short-lived particles, or rather pairs of particles and antiparticles that spontaneously appear, only to recombine and annihilate each other. Normally, these “virtual particles” don’t last long enough to be detected. However, if a photon (particle of light) and an antiphoton appear just outside the event horizon of a black hole, and the antiphoton falls into the black hole, while the photon doesn’t, then the photon doesn’t get annihilated. Thus, Hawking predicts that there should be a net flow of antiphotons into a black hole and photons away from the black hole—meaning the black hole will have a faint glow. This glow is called “Hawking radiation.”

(Shortform note: There are at least two ways to explain Hawking radiation. In the book, Hawking describes this phenomenon in terms of particle-antiparticle pairs, but in his original scientific paper, he used an energy-density approach to calculate the radiation produced near a black hole. Some authors have criticized him for explaining it differently in his book than in the original paper because the quantum energy density approach provides additional insights. In particular, the quantum energy fields allow you to calculate the actual amount and distribution of radiation, and it turns out that Hawking radiation is produced not just on the surface of the event horizon, but in a region around the black hole about fifteen times the size of the event horizon.)

Question 5: Can You Build a Time Machine?

Writers of science fiction have long contemplated the idea of a time machine: a device that allows you to travel forward or backward in time to any point in history or the future. You’re already traveling forward through time, but Hawking thinks it's unlikely that you’ll ever be able to go back. He addresses the possibility of backwards time travel from three different angles: general relativity, quantum mechanics, and wormholes.

Time Travel via Speed

As we discussed in Question 1, the theory of relativity implies that as you approach the speed of light, you’ll move faster through space and slower through time. Hawking points out that, extrapolating this principle, if you could travel faster than the speed of light, you would actually travel backwards in time. However, he also points out that, according to the theory of general relativity, nothing can travel faster than light, so nothing can go backwards in time.

Using Time Dilation for Pseudo-Backwards Time Travel

Hawking shows that relativity doesn’t let you literally go back in time, but he doesn’t explicitly discuss the possibility of going back in time relative to someone else, which is clearly possible based on his early explanation of time dilation.

To illustrate this, imagine that you and your sister have both signed up to emigrate to a new colony on a planet that’s a thousand light-years from earth. The two of you board different starships, and blast off at the same time. Your sister’s ship makes the trip at a speed of 99.99995 percent of the speed of light, while your ship only travels at 99.9992 percent of the speed of light.

From Earth’s perspective, the trip takes about a thousand years for each of you, with your ship arriving just a few days after your sister’s ship does. However, during the trip, your sister ages one year, while you age four years. So, if your sister was two years older than you when you left, she’ll be a year younger than you when you arrive. The effect on your relative age is the same as if you’d gone backward in time three years. So, in a sense, you could say you’ve traveled backwards in time relative to your sister.

Time Travel in Quantum Mechanics

Hawking asserts that, according to the theory of quantum mechanics, it is possible for microscopic particles to travel backwards through time. This is because, in quantum mechanics, a particle moving forward through space and time is mathematically equivalent to its corresponding antiparticle moving in the opposite direction through space and time.

(Shortform note: Hawking doesn’t discuss any practical methods of deliberately converting a particle into an antiparticle, much less intentionally sending a subatomic particle back in time. And the fact that you may be mathematically equivalent to a person made up of antimatter moving backwards through space and time doesn’t really give you a way to move backward in time. Thus, we infer that the practical applications of quantum time travel are quite limited.)

Time Travel via Wormholes

Hawking reports that, according to the theory of general relativity, it’s possible for a bridge to form between warped regions of spacetime, potentially creating an alternate pathway between points in time and space. These hypothetical pathways are called “wormholes.” According to Hawking, wormholes might be your best bet for traveling back in time, because, hypothetically, you could travel forward in time as you go through the wormhole, but arrive at a point in the past when you come out the other end.

However, he cautions that this possibility is still quite remote, for two reasons:

1. Hawking asserts that wormholes are extremely unstable. If any mass (such as a person or a vehicle) entered the wormhole, its gravity would affect the curvature of spacetime enough to cause the wormhole to collapse.

2. Hawking explains that wormholes require spacetime to have concave curvature. The presence of a massive body causes convex curvature of space, resulting in gravity, but scientists have never observed concave curvature of space. So, in practice, it may not be possible to create a wormhole in the first place.

(Shortform note: Hawking doesn’t explain why wormholes require spacetime to be concave, but we infer that it’s just a matter of geometry. Think of a physical tunnel. The walls have to be concave for there to be space inside the tunnel. Presumably it works the same with wormholes, except that spacetime itself is curved.)

Shortform Introduction

Science has profound implications for philosophy and everyday life because science describes and predicts how the universe works. For example, the discovery that time itself had a finite beginning point implies that the physical universe is not eternal, and allows us to infer certain things about its origins.

To make the discoveries and implications of modern science more accessible to everyone, renowned physicist Stephen Hawking described the principles of modern physics for a general audience in A Brief History of Time.

About the Author

Stephen Hawking first became famous in the physics community for his study of “singularities” (a concept we’ll explain later in this guide) in the 1960s, along with George Ellis and Roger Penrose. One of their notable conclusions was that time itself began at a finite point. In 1974, at age 32, he became the youngest scientist ever elected as a Fellow of the Royal Society. He continued to make contributions to the advancement of theoretical physics throughout his life.

However, Hawking’s popularity outside the close-knit community of theoretical physicists was due as much to human factors as scientific brilliance. At age 21, he was diagnosed with ALS, a medical condition that causes motor neurons to degenerate, resulting in loss of motor functions throughout the body. Initially, doctors estimated that he had just a few years to live. Yet, despite using a wheelchair and losing the ability to speak, Hawking remained active in his field. He passed away in 2018, 55 years after his diagnosis.

The combination of his perseverance in the face of disability, his scientific prowess, and his willingness to explain arcane scientific concepts for a general audience propelled him to celebrity status by the late 1980s.

As one of the people who discovered the beginning of time, Hawking is particularly qualified to discuss its origins and history, as he does in A Brief History of Time.

The Book’s Publication

A Brief History of Time was published in 1988 by Bantam Books, an imprint of Random House Publishing. It was Hawking’s first book for a popular audience. It set new records as a best-seller, appearing in the New York Times bestseller list for 147 weeks and in the Times of London list for 237 weeks. To date, it has sold over 25 million copies. Hawking went on to publish a number of other popular books, including The Universe in a Nutshell and Brief Answers to the Big Questions, but A Brief History of Time remains his most popular book.

The Book’s Historical and Intellectual Context

In the twentieth century, new scientific theories changed the way scientists viewed the world. Einstein’s theory of relativity replaced Newton’s laws as a model of gravity for predicting the motion of celestial bodies, and the discovery of quantum mechanics created a new way of modeling the microscopic particles that make up matter and energy. Hawking and his contemporaries built upon these new theories and explored their implications.

In Hawking’s view, philosophers of the twentieth century were unable to keep up with the latest scientific discoveries, even though some of these discoveries had important philosophical implications.

Against this backdrop, Hawking wrote A Brief History of Time to help people outside the physics community understand modern physics, as well as its philosophical implications.

The Book’s Strengths and Weaknesses

Book reviewers unanimously agree that Hawking is a genius when it comes to physics, but they are divided on the question of how well he explains physics to a general audience. Some people find the book an easy and engaging read, while others struggle to understand it.

Critics point out that Hawking sometimes presents conclusions without explaining his reasoning. However, they concede that this was likely because his reasoning was too mathematically involved for a general audience to understand.

Commentary on the Book’s Organization and Approach

Hawking’s approach roughly parallels the order in which these topics would be covered in a college physics program, albeit at a less technical level.

Specifically, the book presents a survey of principles from modern physics, loosely following the order in which they were discovered. It begins with a summary of relevant concepts from classical physics, then goes on to discuss relativity and quantum mechanics, and finally considers some of the more nuanced implications of the new theories, such as the nature of black holes and the possibility of time travel.

In cases where Hawking was personally involved in the scientific investigations, he recounts anecdotes about the circumstances of the discovery. Throughout the book, he also discusses the broader implications of scientific discoveries for philosophy and life.

Our Approach in This Guide

In this guide, we’ve rearranged the discussion around a series of questions that the book addresses. We’ll consider each question in turn, presenting the conclusion up front and then digging into the details and reasons behind it, instead of gradually building up to a conclusion from the details, as the book does.

We’ll also cross-reference the book with other sources, especially in cases where additional scientific data that was collected after the book’s publication may affect Hawking’s conclusions.

Introduction to Formulating Scientific Theories

According to Hawking, the ultimate goal of science is to develop a theoretical model that fully explains how the universe works. Developing theories that explain the universe involves a bit of trial and error. Over time, scientists refine their theories and weed out theories that don’t fit with their observations.

Hawking highlights three characteristics that he says make a good scientific theory:

1. A good theory is consistent with past observations. It should apply to a broad range of circumstances, with as few exceptions or qualifiers as possible. General relativity and quantum mechanics are examples of theories that apply to a wide variety of situations with very few exceptions. Specifically, the theory of general relativity can model the behavior of any set of large-scale objects interacting with gravitational forces. Similarly, quantum mechanics can model the behavior of all kinds of subatomic particles interacting through electromagnetism and nuclear forces. The one exception where these theories can’t be used is when so much mass is concentrated in such a small space that you have to model gravitational interactions and nuclear interactions at the same time. (We’ll talk much more about this later.)

2. A good theory will correctly predict future observations. A theory that doesn’t allow you to make predictions isn’t useful. And if its predictions aren’t accurate, then the theory is probably wrong.

3. A good theory can be tested. If the theory is wrong, you should be able to prove that it’s wrong by showing that its predictions are inconsistent with observable reality. Hawking emphasizes that even one clear example of the theory failing is enough to disprove it. On the other hand, he says it’s generally impossible to prove that a theory is correct, because there could always be some exception that just hasn’t been discovered yet. Nevertheless, the more a theory has been tested and found to agree with observations, the more you can trust that it’s at least approximately correct.

The Scientific Method

Hawking’s discussion on what makes a good theory is basically commentary on the “scientific method.” For background, let’s consider an overview of the scientific method, a six-step process that often leads to the creation of new scientific theories.

Step 1: Observe the world. Science is the study of the natural world.

Step 2: Ask a question. This question serves to focus your study on explaining some aspect of the natural world.

Step 3: Develop a hypothesis, or in some cases multiple hypotheses. Each hypothesis is a tentative answer to your question, based on your observations.

Step 4: Test your hypothesis (or each of your hypotheses). Typically, you test a hypothesis by using it to make predictions. If your hypothesis is true, what does it imply about the natural world? What would you expect to observe if your hypothesis is true? Then you set up an experiment or make additional observations to see if they are consistent with your predictions.

Step 5: Analyze the results. Did your observations match your predictions? If not, go back to step three and modify your hypothesis or come up with a different one.

Step 6: If your hypothesis did allow you to make accurate predictions, continue testing it, and have other people test it to corroborate your results. A hypothesis that has been extensively tested and is widely accepted by the scientific community is called a theory. Historically, what we now call a “theory” was called a “law of nature,” “law of physics,” or just a “law,” so today the terms “law” and “theory” are functionally synonymous.

However, there is no universal standard for just how extensively tested and how widely accepted a hypothesis has to be before it’s considered a theory. Thus, be aware that some people apply the term “theory” to a published hypothesis much sooner than others do. Also note that sometimes theories (and laws) achieve wide acceptance for a time, but later get disproven.

This is where Hawking’s advice on qualities of a good theory comes to bear. If a theory is only accepted as applicable in certain cases because it can’t explain all the existing observations, or if new observations disagree with its predictions, then this implies that it doesn’t provide a very accurate description of the natural world. Similarly, if a theory can’t be tested because it doesn’t allow you to make predictions, then there’s no way of knowing if it's accurate or not.

Question 1: Is Reality Relative or Absolute?

In this Question, we’ll discuss Hawking’s explanation of the relative nature of space, motion, time, and mass.

Relativity in the Big Picture

Philosophers have long argued about whether reality is objective or subjective: If something is true for me, does that make it true for you? Or could your truth be different and yet equally valid? Science is founded on the assumption that reality works the same for everyone: If two scientists conduct exactly the same experiment, they should get the same results.

Ironically, this principle has driven scientists to the conclusion that many things, including motion, position, time, and weight are relative to the observer (or rather to the observer’s frame of reference, which is what you are taking measurements relative to).

Space Is Relative

To illustrate how space is relative, Hawking begins by discussing how ancient theories of absolute space were disproven and then presents the more modern theories that replaced them.

Specifically, he explains that the ancient Greek philosopher Aristotle believed that space and motion were absolute. In other words, there was some frame of reference that all observers could agree was stationary, from which you could measure absolute position or velocity.

Furthermore, as Hawking points out, Aristotle believed that objects would only move when force was applied to them. If the force was removed, they would stop moving. Thus, you could use anything that wasn’t moving as a reference for determining the absolute motion of anything that was moving. Of course, in Aristotle’s day, most people assumed the earth was stationary, so they believed it was an appropriate reference point from which to measure absolute motion (we know now that this isn’t true because the earth isn’t actually stationary—it’s moving through space).

However, Hawking recounts that Italian scientist Galileo Galilei observed objects in motion and found that Aristotle’s theory didn’t agree with observations. To explain Galileo’s observations, English scientist Isaac Newton developed a theory of motion that would come to be known as “Newtonian mechanics.”

Unlike Aristotle’s theory, Newton’s theory predicted that an object in motion would stay in motion unless a force was applied to it to change its course. This challenged the concept of absolute motion, because it implied that objects didn’t naturally come to rest with respect to the absolute reference frame. And since objects didn’t naturally come to rest, there wasn’t any obvious way to establish an absolute reference frame (because everything is always moving).

Overview of Newtonian Mechanics

Hawking’s stated purpose in writing A Brief History of Time is to make modern physics (mostly general relativity and quantum mechanics) accessible to a general audience. As such, he brings up some of Newton’s laws in passing and assumes that the average reader already has some understanding of traditional Newtonian mechanics, which may not be the case for all readers. Thus, to provide additional context, let’s consider an overview of Newtonian Mechanics.

Newtonian Mechanics consists of four principles, known as Newton’s three laws of motion and Newton’s law of universal gravitation. (Some basic definitions: Your “velocity” is your change in position over time, and your “acceleration” is your change in velocity over time.)

Newton’s First Law of Motion states that an object’s velocity will not change unless a force is applied to the object.

Newton’s Second Law of Motion quantifies how much an object’s velocity will change when a force is applied to it. Specifically, it states that the force (F) required to make an object of a certain mass (m) accelerate at a certain rate (a) is given by the equation: F = m x a

Newton’s Third Law of Motion states that whenever objects apply forces to each other, the force on both objects at their point of contact is the same. For example, if you’re pushing your son on a swing, he feels the same amount of force applied to his back as you feel your hands applying to him.

Newton’s Law of Universal Gravitation states that the gravitational force of attraction between two objects is equal to the mass of the two objects multiplied together, divided by the square of the distance between them, and scaled by the gravitational constant.

Newtonian Mechanics Implies Motion Is Relative

As Hawking points out, Newtonian mechanics implies that motion is relative to the observer because there is no absolute reference frame.

Applying Relative Motion to Driving

One familiar scenario where the relativity of speed becomes important is driving a car. To avoid collisions, you have to keep track of the motion of other cars relative to your own. You also have to keep track of your speed relative to the road, since posted speed limits are implicitly specified relative to the road.

To maintain a constant following distance behind another car, you have to adjust your speed to be zero relative to the other car (meaning you’re traveling the exact same speed as the other car). Studies of traffic jams show that traffic jams form because of a chain reaction in how drivers respond to changes in the relative speed of other vehicles. Specifically, if you see the car in front of you slowing down, such that you have to apply the brakes to maintain a relative speed of zero, you’ll instinctively tend to over-compensate. The driver behind you will do the same, and so on, ultimately causing a traffic jam if there’s enough traffic on the road.

Space Is Relative Because Motion Is Relative

Furthermore, as Hawking points out, if motion is relative, then location (or space) is also relative. In other words, we cannot tell, in any absolute sense, whether two events that happened at different times happened at the same location in space.

To illustrate this, imagine you’re driving a car with a leaky sunroof. You just drove through a rain shower, and now water is dripping through the roof onto your head. From your perspective, each droplet of water lands in the same place. However, a pedestrian who watches you drive by sees one water drop hit your head as you pass her, and by the time the next drop hits you, you’re half a block further down the road from her. Relative to the pedestrian, each drip lands at a different location.

(Shortform note: You may not realize it, but you probably think in terms of relative space all the time. Since space is relative, you can only specify the location of something relative to a certain “frame of reference,” such as a landmark. According to professor Barbara Oakley, the human brain is wired to record “visuo-spatial information”—that is, images of objects or scenes and where they’re located relative to each other. Oakley explains that these mental chains of interconnected reference points helped our ancestors to survive as hunter-gatherers. In other words, we’re wired to recognize the relativity of space.)

Time Is Relative

In the same way that the motion of objects and the location where events happen in space is relative to the observer, Hawking argues that different observers may measure time differently. In particular, time appears to slow down for entities that are moving very fast.

Time Is Relative Because the Speed of Light Isn’t

Hawking explains that everyone who accurately measures the speed of light gets the same result, regardless of their particular reference frame, because the laws of physics are consistent for all observers.

(Shortform note: When Hawking refers to “the speed of light,” technically he’s referring to the speed of light in a vacuum. Light slows down slightly when it travels through materials like water or glass. This is what causes refraction of light, where the change in speed at the boundary between two materials causes the light to bend. It also makes Cherenkov radiation possible: Cherenkov radiation is light that is produced when a particle moves through a material (usually water) faster than the speed of light in that material, similar to how an airplane that goes faster than the speed of sound makes a sonic boom. As we’ll discuss, it’s impossible for anything to move faster than the nominal speed of light (that is, the speed of light in a vacuum), but when light itself goes slower through certain materials, particles can sometimes outrun it.)

According to Hawking, this is the case even if the light source is moving relative to you. To illustrate this, first imagine that you’re watching a parade, and someone in the parade throws you a piece of candy. If the parade is moving towards you at three miles per hour (mph), and he throws the candy at 10 mph relative to the float that he’s riding on, then you would measure the speed of the candy at 13 mph, because the speed of the float adds to the speed of the throw. If he waited until after the float passed you, so he was moving away from you when he tossed the candy, you would measure the speed of the candy at seven miles per hour, because then the speed of the float would take away from the speed of the throw.

However, the speed of light works differently than the speed of a physical object. If you measure the speed of light coming toward you from headlights of cars in the parade, and also the light moving away from you from their tail lights, you’ll find that it’s exactly the same: about 186,000 miles per second. This would be the case even if you were watching a parade of starships that flew by at 99% of the speed of light.

Hawking explains that time must be relative because of the relationship between time, speed, and distance. Speed is defined as the distance an object travels in a given amount of time (for example, miles per hour). Since space is relative, time must also be relative for the speed of light to be constant.

For example, imagine two kids playing laser tag on a starship that is traveling at the speed of light. As they fire pulses of light back and forth, from opposite sides of the ship, an observer on the ship measures the distance that the light travels and finds it equal to the width of the ship. But if you’re outside the ship, you would see the light traveling a greater distance. Specifically, the distance would be the hypotenuse of a right triangle, with one leg equal to the width of the ship, and the other equal to the distance the ship traveled while the light was moving across it. Since you perceive the light traveling a greater distance (at the same speed) than the people on the starship, you must also perceive more time elapsing during the event than they do.

The Theories of Relativity

We’ve seen how Newtonian Mechanics implies that space is relative, and how the constancy of the speed of light implies that time is relative. When time progresses at a different rate for one person than another, scientists call this “time dilation.” As Hawking points out, Newtonian Mechanics does not account for time dilation, so Albert Einstein developed his theories of relativity as a replacement for Newtonian Mechanics to remedy this problem. Einstein introduced his theory of relativity in two phases: special relativity and general relativity. Let’s discuss each of these theories in turn.

Special Relativity

First, as Hawking recounts, Einstein developed his theory of special relativity as a model to predict the motion of objects, even at speeds approaching the speed of light. However, he ignored gravity and acceleration to make the mathematical derivation simpler. This allowed him to publish his theory quickly and gain support for it. Hawking notes that French mathematician Henri Poincare published a similar derivation about the same time, which corroborated Einstein’s arguments in support of special relativity.

(Shortform note: “Special Relativity” is “special” because it only works in situations where there is no gravity or acceleration. Physics problems with no gravity or acceleration are simpler, and constitute a “special case,” where a relatively simple theory of relativity can be applied.)

General Relativity and the Curvature of Space

However, scientists needed a more broadly applicable theory of relativity that could account for gravity and acceleration. Einstein spent several years developing his theory of general relativity to meet this need. Like special relativity, general relativity is a theory for predicting the motion of objects that is accurate even for objects moving at speeds close to the speed of light. However, general relativity can model gravity and acceleration, whereas special relativity cannot. In other words, general relativity is more broadly (or “generally”) applicable than special relativity.

As Hawking points out, developing the theory of general relativity required a difficult mathematical derivation, and the key idea that allowed Einstein to complete it was his realization that gravity could be viewed as the curvature of space itself. In other words, general relativity is based on the principle that mass actually causes space to warp, such that the shortest distance between two points is an arc segment, rather than a straight line.

As Newton theorized, an object moving in Euclidean (not curved) space tends to continue moving in a straight line unless a force is applied to it. However, as Hawking explains, if space is curved, then the straight line becomes an arc. The object then continues along a curved path, as if a force were deflecting it, so the curvature of space is equivalent to the force of gravity.

Hawking points out that light also follows the curvature of space, so that, for example, light from a distant star that passes through the gravitational field of another star on its way to earth will bend, making the star appear to be in a different place.

Testing General Relativity

Initially, Einstein’s theory of general relativity was somewhat controversial, mostly because of its implications about the origin of the universe, which we’ll discuss in Question 3. Because of the controversy, it was subjected to even more testing than most theories, and, so far, all the test results have agreed with the predictions of general relativity.

Since general relativity is a theory of motion and gravity, most tests of the theory involve using it to predict the motion of astronomical bodies like planets, stars, and black holes (we’ll discuss black holes more in Question 5) and comparing these predictions with observations.

The first widely-publicized test of general relativity came in 1915, when Einstein used his theory to predict the orbit of the planet Mercury. He predicted that the orbit would be slightly different from what Newtonian Mechanics predicted—and he was right. In fact, it turned out that astronomers who had been mapping Mercury’s orbit had been puzzled over its deviation from Newtonian Mechanics since 1855. (Some astronomers thought there must be another planet orbiting between Mercury and the sun that was disrupting Mercury’s orbit. They had even tentatively named the hypothetical planet Vulcan, but in 60 years of observations, they never managed to detect it.)

More recently, general relativity has been tested using LIGO, the Laser Interferometer Gravitational Observatory, which detects gravity waves. General relativity predicts that since gravity is the curvature of space, massive objects moving through space should create ripples in spacetime. These ripples are called gravity waves. The heavier the objects and the faster they move, the more gravity waves they produce.

Researchers at LIGO have observed gravity waves from colliding black holes. These provide a particularly good test of general relativity because the waves are very strong, making them easier to detect and accurately measure. As the black holes collide, their speed also approaches the speed of light, allowing scientists to test the predictions of general relativity at relativistic speeds. So far, the gravity waves from colliding black holes that have been detected have matched the predictions of general relativity.

Further Implications of Relativity

Mass Is Relative

Hawking explains that, as an object accelerates to speeds closer and closer to the speed of light, its mass increases, such that it can never actually reach the speed of light.

As Hawking points out, it takes energy to increase the speed of something, and the more massive it is, the more energy it takes to increase its speed by a given amount. For example, think about a slingshot: When you pull it back, you store a certain amount of energy in the rubber bands. When you release them, the energy is transferred to the pebble in the pouch of the slingshot, accelerating it to a high speed. But if you put a heavier pebble in the slingshot, its speed will be slower, because it would take more energy to accelerate it to the same speed as the lighter pebble.

Hawking explains that, as a consequence of relativity, there is a relationship between energy and mass. This relationship is expressed in Einstein’s famous equation E=mc², where “E” is energy, “m” is mass, and “c” is the speed of light. Hawking notes that the speed of light is constant, so as energy increases, mass must also increase.

Shortform Note on E=mc²

While it serves to illustrate the concept, the equation E=mc² does not actually let you calculate the mass of a fast-moving object. The equation for calculating relativistic mass is:

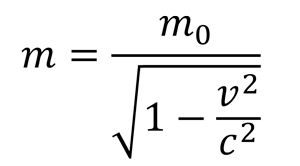
In this equation “m₀” is the “rest mass” (mass when the object isn’t moving), “v” is its speed, and “c” is the speed of light.

Note that the change is proportional to the ratio of the object’s speed to the speed of light. You’ve probably never noticed anything getting heavier as it speeds up, because the speeds you encounter in everyday life are so small compared to the speed of light that the change is negligible. For example, suppose you accelerate an airplane weighing 100 tons to 1000 mph. At this speed, its mass would increase by about 0.0001 grams.

Why an Object Can Never Travel at the Speed of Light

As Hawking explains, the more energy you apply to something to increase its speed, the more you increase its mass, and the more mass it has, the more energy it takes to further increase its speed. Consequently, it would take an infinite amount of energy to accelerate anything that has mass to the speed of light. (Of course, light doesn’t have mass, which is why it travels at the speed of light.)

Alternative Explanation

Experimental data from particle accelerators conclusively demonstrates that, as the speed of a particle increases, the energy required to further increase its speed also increases, just as the theory of relativity predicts.

However, some scientists have argued that this is not because the mass of the particle increases, but rather because the efficiency of energy transfer decays as the speed of the particle approaches the speed of the forces that you’re using to accelerate it.

To illustrate this principle, imagine a sailboat that’s initially standing still. When you first hoist the sails and catch the wind, the force of the wind against the sails is strong, and the boat accelerates. However, as the speed of the boat starts to approach the speed of the wind, the wind no longer pushes on the sails as hard, and the acceleration of the boat tapers off. If the sailboat could go the same speed as the wind, then the wind would no longer apply any force to the sails.

Similarly, forces like gravity and magnetism travel at the speed of light. You can think of the force applied to an object as a flow of massless carrier particles (photons for electromagnetic forces, gravitons for gravitational forces) from the source of the force to the object. As the speed of the object approaches the speed of light, the amount of force that the force carrier particles can apply to it tapers off.

From the standpoint of someone trying to accelerate something to the speed of light, this has much the same effect as if the object’s mass was increasing, since it becomes more difficult to accelerate as it gets closer to the speed of light. But, according to this alternate interpretation, this is because the object feels less force as its speed approaches the speed of the force that’s being used to accelerate it, and its mass actually stays the same.

Time Is Relative to Gravity

We’ve discussed how motion, space, and even time are relative to your frame of reference, and how the mass of an object also seems to be relative to its velocity. Hawking explains that the theory of relativity also implies that time is relative to gravity.

Specifically, time slows down for people who are experiencing high gravity just like it does for people who travel very fast. Thus, a person living on the top floor of a tall apartment building will age faster than someone living on the ground floor because the person on the ground floor is closer to the earth, where the earth’s gravity is stronger.

(Shortform note: You’ve probably never noticed a difference in the passage of time at high elevation versus low elevation because the difference is very small. There are two reasons for this: First, Earth’s gravity only decreases by about 0.03% per kilometer of elevation that you gain. Second, Earth’s gravity is very weak by relativistic standards, so even the time dilation between zero-gravity and Earth’s gravity is not enough to notice intuitively. However, there are clocks precise enough to measure the difference. In fact, the National Institute of Standards and Technology (NIST) has atomic clocks capable of measuring time dilation with just one foot of elevation difference between them.)

Answer Recap

So, is reality relative or absolute? Well, the laws of physics are formulated to be the same for everyone, so they’re absolute in the sense that they’re not relative to the individual. In particular, the speed of light is the same for all observers, regardless of how fast you or the source of the light is moving. However, motion, position, time, and even mass are all relative.

Question 2: Is the Future Predetermined?

As we have seen, scientific theories allow us to model the behavior of objects and make predictions about future observations or the outcomes of experiments. Hawking points out that if we could formulate a unified theory of physics that could be applied in any context, then if we knew the exact state of the entire universe at any point in time, we could use the theory to predict the state of the universe at any other time. This would make human free will an illusion, since we could calculate everyone’s future actions. Hawking refers to this as “scientific determinism.”

However, Hawking also discusses three limitations of scientific determinism:

Scientists have not yet been able to find a unifying theory of physics.
The theory of quantum mechanics (one of the major theories in modern physics) gives results in terms of probability, rather than deterministic results.
The uncertainty principle of quantum mechanics limits our ability to measure the state of the universe at any given time, so even if you had a unified, deterministic theory, you couldn’t measure the present state of the universe accurately enough to exactly predict its future state.

In the remainder of this Question, we’ll examine each of these limitations in more detail.

No Unifying Theory

Hawking asserts that the ultimate goal of science is to develop a “unifying theory” that can be applied in any context. Scientists have made progress towards this goal, but have not yet achieved it. Instead, scientists currently use two major theories: general relativity and quantum mechanics. Each of these theories makes accurate predictions when applied in its intended context, but the intended context of the two theories is very different. Additionally, if you try to apply both of them in one of the rare cases where their applicable context overlaps, you run into problems. Let’s discuss the limitations of each theory as well as some of the attempts to create a unified theory.

The Limitations of General Relativity

To accurately model the motion of objects as they approach the speed of light, Hawking says we must use the theory of general relativity. This theory works great for predicting the motion of stars, planets, and macroscopic (big enough to see without a microscope) objects in general. However, Hawking notes that relativity does not accurately model the behavior of subatomic particles. The reason for this has to do with the nature of particles, which we’ll discuss next.

The Wave-Particle Duality of Particles

Hawking explains that small particles exhibit “wave-particle duality,” which means that in some ways they act like particles, traversing distinct paths, but in other ways they act like waves propagating through space. The theory of relativity can only model particles as objects that follow deterministic paths through space, so it doesn’t take into account the wave part of their nature.

As an example of particles acting like waves, Hawking describes the famous double-slit experiment. In this experiment, a shield with two parallel slits in it is placed in front of a detector screen. Particles of matter or energy, such as photons or electrons, are fired at the screen. This results in an interference pattern (or alternating bands of light and dark) showing up on the detector screen, because the two slits act like two separate wave sources: Where the crests of both waves line up, they add to each other, and more light registers on the detector screen. Where the crest of one wave lines up with the trough of the other, they cancel each other out, and less light registers on the detector screen. Hawking observes that the interference pattern appears even if the particles are only fired one at a time. This implies that every single particle goes through both slits at once, like a wave.

(Shortform note: To visualize how a wave passes through both slits at once, imagine a beach with a sea-wall protecting a swimming area. There are two open gates in the wall. An ocean wave rolls in and hits the wall, passes through the two gates, and fans out inside the swimming area.)

The interference would not happen if the particles acted like solid objects that can only pass through one slit or the other. General relativity doesn’t accurately model the behavior of small particles because it doesn’t allow for modeling wave interference between objects.

Modern Wave-Particle Duality Experiments

Since the publication of the book, scientists have repeated the double-slit experiment not only with subatomic particles, but with various atoms and even large molecules. Performing the experiment with whole molecules is challenging, because you need a source of particles that have uniform mass and velocity.

To achieve this, researchers start by heating a very pure sample in a special container with a vent that directs a jet of vapor into a vacuum chamber. In the vacuum chamber, the molecules follow curving paths due to the pull of gravity, and the exact curvature depends on their velocity. Thus, all the molecules that impact the far wall at a certain elevation have the same velocity. A slit in the wall allows the molecules with the desired velocity to continue into the chamber housing the double-slit experiment. In this way, researchers have tested molecular compounds containing over 800 atoms per molecule and have found that even these molecules show interference patterns consistent with wave behavior.

The Limitations of Quantum Mechanics

Like the theory of relativity, the theory of quantum mechanics has limitations that prevent it from being a unifying theory. Unlike relativity, quantum mechanics accurately models the behavior of subatomic particles and their interactions with electromagnetic and nuclear forces. However, according to Hawking, quantum mechanics doesn’t allow for modeling gravitational interactions or macroscopic objects.

As Hawking explains, the reason quantum mechanics doesn’t provide a model of gravity is that the mass of the subatomic particles that we can observe is so small that the effect of their gravitational attraction to each other is too small to measure. However, we can’t simply add more particles to make them easier to measure: According to Hawking, as the number of particles in a quantum-mechanics problem or simulation increases, the complexity of the calculations also increases. It takes so many atoms to build even a speck of dust that the problem becomes too complex to solve.

(Shortform note: Other authors tend to agree with Hawking that quantum mechanics can’t model gravity because the math is too complicated, but some offer different explanations for why this is the case. For example, astrophysicist Paul Sutter explains that, when calculating particle interactions in quantum mechanics, scientists assume that space is Euclidean (not curved) and is not affected by the particles. These calculations are already complicated, and if you instead assume that the mass of the particles causes space to curve (as general relativity predicts) then that adds a whole new dimension of complexity, making the math problem insoluble.)

Attempts to Unify Relativity and Quantum Mechanics

Hawking reports that no one has yet been able to come up with a theory that incorporates both quantum mechanics and general relativity.

He explains that part of the problem is that combining the equations from the two theories results in predictions that clearly contradict observations, such as gravity being infinitely strong everywhere. A theory called “supergravity” partially solved this problem by modeling particles differently, such that they were all variations of a “super-particle.” However, Hawking reports that the predictions of supergravity theory didn’t match observations of actual particles, and the mathematics of the theory were also too complicated to be practical.

According to Hawking, “string theory” is the most promising possibility for unifying quantum mechanics and general relativity. He explains that the premise of string theory is that all fundamental particles can be modeled as microscopic loops of one-dimensional “string” that vibrate in multiple directions. He notes that these “strings” would have to vibrate in ten or more dimensions to explain all the observed properties of particles, but that we only perceive four dimensions on a macroscopic scale (three spatial dimensions and one time dimension) because the other dimensions are curled up into tiny closed loops.

(Shortform note: Although there has been a great deal of work done on string theory and M-theory (which is a superset of string theory) since Hawking wrote A Brief History of Time, actual progress has been minimal. Many physicists still consider it the most promising approach to unifying general relativity with quantum mechanics, but a complete mathematical model has yet to be formulated. As such, there is no experimental evidence to support it, because you need a complete theory before you can use it to make testable predictions.)

Is Thermodynamics the Unifying Theory?

In 2011, Pharis E. Williams published a book on “Dynamic Theory,” which allegedly provides a simple yet powerful way to unify quantum mechanics and general relativity. The essence of Williams’s approach was to generalize the first and second laws of thermodynamics in five dimensions: three dimensions of space, one of time, and one of mass.

In thermodynamics, there are methods for calculating how a system (such as a steam power plant) will respond to being jostled. Williams adapted these methods to provide a model of motion.

Williams explains that if you apply his model to the special case where entropy is constant, then certain terms drop out, and it reduces to the equations of quantum mechanics. If you instead apply it to a different special case where mass density is conserved, different terms drop out, and it reduces to the equations of general relativity. If you don’t assume either special case and keep all the terms in Williams’s model, then it appears to provide a unifying theory that’s universally applicable.

However, Williams’s theory has yet to be rigorously tested. Williams (who passed away in 2014) used his theory to make many predictions, but most of them have not been investigated experimentally. This may be partly because Williams was an outsider to the mainstream physics community (he worked mostly as an ordnance engineer for the US Navy), and thus lacked the professional connections to raise funding and support for experimental studies of his theory.

Probability and Quantum Mechanics

As we’ve discussed, quantum mechanics is able to accurately model the behavior of subatomic particles because it takes into account the wave-particle duality of matter and energy. However, using quantum mechanics imposes another limitation of scientific determinism, because quantum mechanics doesn’t provide deterministic solutions.

Hawking explains that if you model the motion of a particle with quantum mechanics, you get a probability map, showing you where the particle is most likely to go and where it is less likely to go. He explains that this is because, to model the wave-particle duality of matter and energy, the theory assumes that a particle simultaneously travels every possible path that it could take. The probability map comes from calculating how waves taking these different paths would interfere with each other.

(Shortform note: There is a connection between the mathematical field of statistics and the theory of quantum mechanics because quantum mechanics provides probabilistic solutions instead of deterministic ones. However, statistical mathematics used in quantum theory is different from what’s used in traditional statistics. This is mostly because traditional statistics usually deals with only one or two variables at a time, while quantum theory has to manage a larger number of variables at once. Nevertheless, mathematicians are beginning to adapt methods from quantum mechanics to general statistical modeling. This is creating new mathematical tools for statistical analysis and new types of statistical metrics.)

The Uncertainty Principle

We’ve discussed how quantum mechanics provides probabilistic solutions instead of deterministic ones and how that limits scientific determinism. But there’s another limitation on determinism that comes from quantum mechanics as well: the uncertainty principle.

As Hawking explains, the uncertainty principle states there is always at least a certain amount of uncertainty in your measurement of the position and velocity of a particle. This is important because to predict where a particle will go (or is most likely to go) in the future, you need to know where it was and which way it was going at some point in the past or present. Uncertainty about the present creates greater uncertainty about the future.

(Shortform note: Hawking explains how uncertainty can limit the accuracy of your predictions in physics, but this general concept is applicable to other areas as well, especially in fields like the social sciences where outcomes are harder to measure or quantify. In his book Superforecasting, Philip Tetlock discusses the importance of measurement in predicting the future. In particular, he points out that many political and economic forecasters’ predictions are never actually checked against measurements after the fact. This makes it difficult to assess the credibility of the forecaster or the accuracy of their methods.)

To understand how the uncertainty principle works, you need to understand a few things about quantum mechanics. For one thing, as Hawking notes, a basic premise of quantum mechanics is that certain quantities like energy and frequency have to be incremented by at least a certain minimum value. (Shortform note: This minimum unit is called a “quantum” of energy, which is where “quantum mechanics” gets its name.)

To explain this phenomenon, it’s helpful to consider how quantum mechanics was discovered, so let's discuss its origins. Then, we’ll show how quantum mechanics gives rise to the uncertainty principle.

The Origins of Quantum Mechanics

Hawking recounts that circa 1900, scientists realized that their theories of radiant heat transfer predicted that any hot object should radiate an infinite amount of energy, which was obviously not the case. The reason was that in these theories, radiation could have any frequency, and objects were thought to give off radiation uniformly over a range of frequencies.

For example, a hot object might give off radiation at 10 Mhz, 10.1 MHz, 10.01 Mhz, and so on. Mathematically, there are an infinite number of frequencies between 10 and 11 MHz (or any two frequencies), so if the object radiates energy at every possible frequency, then it will give off an infinite amount of energy.

Hawking explains how, to resolve this problem, Max Planck hypothesized that physical quantities like the frequency of radiation are “quantized,” meaning they can only have certain distinct values. If frequency could only be incremented by a finite value, then an object would only give off a finite amount of radiation because there would only be a finite number of frequencies at which it could give off radiation. This solved the problem and led to the development of the theory of quantum mechanics.

Shortform Note: Standing Waves and Quantization

As Hawking recounts, Planck was the first to recognize that electromagnetic energy was quantized, and Planck may have coined the term “quantum.” However, in Planck’s day, it was already common knowledge that certain physical quantities were “quantized,” in the sense that they could only have certain values.

In particular, the harmonics of standing waves are quantized, as Pythagoras described around 500 BC. If you pluck a guitar string (or any string stretched between two fixed points) it will only vibrate at certain frequencies, called harmonics. This is because the fixed ends of the string constrain it, such that it can only support waves if the length of the string is equal to half the wavelength of the wave, or a whole-number multiple of this length. So, if your guitar string is 24 inches long, it will only vibrate at frequencies that correspond to waves with a wavelength of 48 inches, 24 inches, 16 inches, 12 inches, 9.6 inches, and so on.

Today, physicists often describe an electron’s orbit around an atom’s nucleus as a type of standing wave and use this to explain the quantization of electromagnetic energy.

Quantum Uncertainty

But how does the fact that frequency is quantized give rise to the uncertainty principle? It has to do with the way light disturbs particles.

As Hawking explains, you can only see something if it is reflecting (or otherwise emitting) light. If there’s no light, you won’t be able to see it. The same principle applies to measuring subatomic particles: The instruments that measure their position and velocity can only “see” them by bouncing light (or other particles, like electrons) off of them.

However, according to Hawking, this imposes fundamental limitations on the accuracy of the measurement, because bouncing photons or electrons off of a subatomic particle will change its velocity. The higher the frequency of the light bouncing off a subatomic particle, the more energy its photons have, and the more it will change the velocity of the particle you’re trying to measure. The frequency is also inversely proportional to the wavelength, and the light that bounces off the particle will only indicate its position to the nearest wavelength.

Thus, if you use very high-frequency light, you can measure the particle’s position very accurately, but you’ll disrupt its velocity so much that you get no useful information about its velocity. If you use very low-frequency light, you can measure its velocity accurately, but not its position. If you use an intermediate frequency, you can measure both position and velocity with an intermediate amount of uncertainty, but your total uncertainty will always be at least a certain value.

Measurement Error Versus Quantum Uncertainty

It is important to distinguish between ordinary measurement uncertainty and quantum uncertainty.

In real life, every measuring device has limited precision. For example, imagine you’re trying to measure the length of a metal rod. If you measure it with a ruler, your measurement is only as accurate as the marks on the ruler. Say your ruler is marked in sixteenths of an inch, so your measurement is only certain to the nearest sixteenth of an inch. If you measure it with a dial caliper instead, you can get a more accurate measurement, but your measurement will still have a few thousandths of an inch of uncertainty. With increasingly precise measuring tools, you can reduce the uncertainty in your measurement.

The same principle generally applies to measuring position, velocity, or anything else that you might want to measure: The better your measuring tools, the less uncertainty there will be in your measurement.

When it comes to measuring the position and velocity of subatomic particles, the precision of your measuring instruments is still important. But, as we’ve discussed, the uncertainty principle imposes additional limits on your ability to determine both the position and velocity of a particle. So even in the hypothetical case where you had perfect measuring tools, there would still be uncertainty in your measurement (and any measurement uncertainty from your instruments gets added to the quantum uncertainty).

Answer Recap

So, is the future predetermined by the laws of physics? Well, it might be, if there is a theory that completely defines how the universe works. But so far, scientists have not been able to find such a theory.

Exercise: Analyze an Unpredicted Event

As we discussed, scientific theories allow you to predict the future, given enough information about the present. However, this predictive power is limited in two ways: There’s currently no theory that can model everything, and quantum uncertainty limits how much you can know about the present. In this exercise, you’ll have a chance to analyze how these principles apply to your life.

Think about the last time you experienced something unexpected. Briefly describe what happened.
Did it change your mental model of how the universe works? In other words, did it change the way you think about the world or how you expect the future to unfold? Why or why not?
Why was it unexpected? What information would you have needed to predict it in advance?
In hindsight, would you say the event was “deterministic,” or bound to happen, given the causes that led up to it, or could it just as easily have turned out differently? Why?

Question 3.1: How Did the Universe Begin?

Hawking points out that the origins of the universe have profound philosophical implications. He contrasts the Judeo-Christian belief that God created the universe with the atheistic view that many scientists held in the nineteenth century, namely that the universe was infinite and had always existed. Since the universe had always existed, there was no need for a divine creator to bring it into existence. Hawking refers to this view as the “static universe model.”

Hawking recounts that in the twentieth century, new scientific discoveries challenged the theory that the universe had always existed. Based on these discoveries, the “big bang” theory ultimately replaced the static universe model. The big bang theory posits that the universe is expanding outward from a point where it came into existence at a finite time in the past.

The big bang theory presented two significant philosophical problems for Hawking and other atheist scientists. First, the idea that the universe had a beginning seemed uncomfortably similar to the Judeo-Christian concept of creation. Second, the theory arguably implied that the universe was fine-tuned for humankind, because the big bang model was extremely sensitive to initial conditions, such as its expansion velocity and the distribution of matter. If any of these initial parameters had been even slightly different, the universe would not have been able to support human life. However, Hawking argues that these problems can be addressed by considering the implications of quantum mechanics.

In this Question, we’ll first review the discoveries that led to the development of the big bang theory, as Hawking presents them. Then, in the next chapter, we’ll discuss the issue of fine-tuning and the quantum approach that Hawking proposes to remove the fine-tuning requirement.

Contrasting Religious Perspectives on the Big Bang

As we discussed, Hawking saw a similarity between the big bang theory and the Judeo-Christian idea of creation, and he found this similarity concerning because he was an atheist. Some atheists share Hawking’s concerns about the big bang theory, but others do not. A common perspective among atheists is that the big bang theory is an atheistic creation story. They see no reason to assume that the big bang singularity required God to create it or set it in motion. Instead, they point out that every society develops some kind of explanation for the origins of the world, and argue that the big bang theory is the most scientifically defensible origin story yet.

A similar difference of opinion exists among creationists. The Catholic Church endorsed the big bang theory as being consistent with the biblical creation. In fact, in the 1920s, a Catholic priest by the name of Father Lemaitre (who also had a background in astronomy) was arguably the first real proponent of the big bang theory.

Some protestants also endorsed the big bang, but many rejected it as an atheistic creation story. This was largely due to the popularity of Ussher’s chronology, which taught that God created the earth (and presumably the whole universe) in the year 4004 BC. Proponents of Ussher’s chronology rejected the big bang theory because it implied that the universe was billions of years old instead of a few thousand years old.

Evidence for the Big Bang

The primary piece of evidence that led to the development of the big bang was the discovery that the universe is expanding. Hawking notes that astronomer Edwin Hubble made this discovery in the 1920s, when he measured the distance to a number of galaxies and found that they were all moving away. Furthermore, the galaxies that were farther away were moving away faster.

Hubble’s Red-Shift Measurements

Hawking explains Hubble’s method of distance measurement, which led to his discovery that the other galaxies were moving away.

Specifically, as Hawking explains, astronomers can measure distances to nearby stars directly, but these methods don’t work for objects that are too far away, such as distant galaxies. However, a light source of a given brightness appears dimmer the farther away it is, so if you know its actual brightness, you can calculate how far away it is by measuring its apparent brightness.

Hawking describes how Hubble was able to estimate the absolute brightness of distant stars by assuming they would give off about the same amount of light as nearby stars that had the same composition. He knew the absolute brightness of the nearby stars because the distance to them had already been measured directly, and he could analyze the composition of a star by passing its light through a prism.

As Hawking explains, when starlight is passed through a prism, it produces an “absorption spectrum” consisting of a pattern of light and dark bands. Dark bands at certain frequencies indicate the presence of certain elements.

Hawking relates how, as Hubble was taking his measurements, he noticed that the characteristic absorption bands of elements in the distant stars were uniformly shifted toward the red (lower-frequency) end of the spectrum.

Hawking goes on to explain that this “red-shift” is produced by the doppler effect: When a source of waves (such as light or sound) is moving relative to the observer, the waves that are going in the same direction get compressed and the waves going in the opposite direction get stretched. This makes the frequency of the waves higher in front of the source and lower behind it. Thus, light from an object that is moving away from you shows a frequency shift toward the red end of the spectrum, and the amount the frequency shifts is proportional to the speed of the object.

Hawking notes that when Hubble took his measurements, he was able to determine both the distance to stars in distant galaxies and their speed relative to earth, because their absorption spectra showed him both their composition (from which he could estimate absolute brightness) and the red-shift, which allowed him to calculate how fast they were moving away from earth.

Hawking recounts that based on Hubble’s measurements, practically all other galaxies were moving away from our own, and the further away they were, the faster they were moving away. Hubble concluded that if other galaxies are all moving away from us, the universe must be expanding.

Methods of Measuring Astronomical Distances

As we discussed, Hubble’s distance measurements relied on knowing the distance to relatively close-by stars, so he could determine their absolute brightness and compare it to the brightness of similar stars in distant galaxies. How did astronomers measure the distance to these nearby stars in the first place?

The answer is triangulation. If you have a triangle, and you know the length of one side and two of the angles, you can calculate the third angle and the length of the other two sides. Astronomers use the diameter of Earth’s orbit as the base of a triangle. They measure the angular position of a star very precisely. Then they wait exactly half a year and take the same measurements again. This gives them the two angles that they need and thus, combined with the diameter of Earth’s orbit, allows them to calculate the distance to the star.

Sometimes the triangulation method is also referred to as the “parallax” method because of the way astronomers measure the angles. If you take a picture of an object from two different positions, the position of the object in the picture will shift slightly, relative to other objects that are closer to you or further away. This relative shift in position due to the change in angle is called “parallax.” Astronomers measure the angle by measuring the parallax.

Double-Checking Hubble’s Measurements With Binary Stars

More recently, astronomers have developed another way of determining the distance to distant galaxies. This provides a second check on Hubble’s method. It only works with binary stars whose orbits are aligned so that, from our vantage point, they pass in front of each other. By observing these “eclipsing binary stars,” astronomers can determine how fast they orbit each other. With this information, they can use general relativity to calculate the mass and absolute luminosity of the stars. Then they can compare this to the stars’ observed brightness to determine how far away they are, just as Hubble did.

The binary star method corroborates Hubble’s method, because it provides another way to estimate stars’ absolute brightness, independent of looking at their composition.

Theoretical Support

Hawking points out that, in hindsight, Hubble’s discovery that the universe is expanding could have been predicted based on general relativity, or even Newtonian mechanics. In fact, Hawking relates that Russian physicist Alexander Friedmann did use general relativity to accurately predict Hubble’s discovery a few years prior to it.

Hawking explains that if the universe was not expanding, then gravity would eventually cause it to collapse in on itself. Thus, scientists as far back as Newton should have known all along that the universe was not static or eternal, but rather it must be either expanding or contracting.

(Shortform note: Historically, scientists justified a static universe model based on gravitational equilibrium. The universe didn’t have to expand or contract because every galaxy was being pulled in every direction equally by the gravity of other galaxies. This, in turn, was because the distribution of matter in the universe was uniform on a large scale, and the universe was infinite in size.)

Hawking recounts how Einstein recognized this when he was developing his theory of general relativity, but at the time, the static universe model was so entrenched in the scientific community that Einstein introduced a hypothetical constant into his equations to cancel out the expansion that his theory predicted. He called this fudge factor the “cosmological constant.” Later, when Hubble’s observations confirmed that the universe actually was expanding, Einstein publicly admitted that introducing this hypothetical constant was a mistake.

The Cosmic Microwave Background

As Hawking explains, physics predicts that there was a period of time where the early universe was small, hot, and dense. The discovery of the cosmic microwave background provided direct observational evidence for this.

Specifically, as we discussed in Question 2, hot objects give off radiation, you can calculate the radiation that an object emits using quantum mechanics. According to Hawking, in the 1960s, physicists Bob Dicke and Jim Peebles calculated that radiation from the early universe should still be detectable. Because of the subsequent expansion of the universe, it would be red-shifted into the microwave range of the electromagnetic spectrum and would be very faint. They also predicted that it should come from every direction uniformly, since, at that time, the matter in the universe was very uniform; stars and other objects hadn’t formed yet.

(Shortform note: Physicists are continuing to refine this theory. Dicke and Peebles originally assumed that this microwave background should be completely uniform, but others eventually pointed out that there should be slight variations, since you need areas of slightly higher density in order for matter to eventually collapse under gravity and form stars and galaxies. These slight variations have since been observed and mapped using satellites. Recently, new measurements showed that the cosmic microwave background is also slightly brighter in one half of the sky than the other. Theorists are still exploring possible explanations for this.)

Hawking also tells how, about the same time that Peebles and Dicke did their calculations, astronomers Arno Penzias and Robert Wilson were trying out a very sensitive microwave antenna when they discovered faint, uniform microwave radiation that seemed to come from every direction. Initially, they thought it was some kind of noise or interference, but after extensive troubleshooting they were able to rule out the possibility that it came from the detector itself or a source inside Earth’s atmosphere.

According to Hawking, Penzias and Wilson eventually connected with Dicke and Peebles and realized that they had been picking up the radiation from the early universe. This radiation was later dubbed the “cosmic microwave background.”

Question 3.2: The Fine-Tuning Problem

Hawking relates how, as scientists continued to refine the big bang theory, their models implied that the initial conditions of the universe (like its initial rate of expansion, density and uniformity, and so forth) would have to be exactly right for habitable planets to form. If any of the physical parameters of the big bang had been even slightly different, human life would never have been possible.

For example, if the initial expansion rate of the universe was too high, all the matter would have dispersed too quickly for stars and planets to form. If it was too low, gravity would have caused it to collapse again before life-supporting planets could form. Hawking points out that we observe the universe expanding at approximately the “critical rate,” that is, the maximum rate at which it could eventually re-collapse.

(Shortform note: We infer that this is important because it would give stars and planets the greatest window of opportunity to form, since any less would cause the universe to collapse in on itself sooner, and any more would remove the materials that are needed for star formation more quickly.)

To Hawking, the need for fine-tuning of the initial conditions indicates a problem with the theory, because the theory seems to predict that human life in our universe is extremely improbable, and yet we observe that human life exists. Hawking discusses two different approaches to addressing this problem, namely anthropic principles and the inflationary big bang model, but concludes that neither approach completely resolves the problem.

Anthropic Principles

Hawking presents two different types of “anthropic principles.”

The weak anthropic principle (WAP) states that you observe the universe having the right parameters to allow your existence because if it had different parameters that didn’t allow you to exist, you wouldn’t be here to observe it. Hawking acknowledges that the weak anthropic principle is true, but points out that it doesn’t really explain why the universe is the way it is.

(Shortform note: Although he doesn’t say so explicitly, Hawking’s dissatisfaction with the WAP may stem from the fact that it doesn’t satisfy his requirements for a theory. Recall Hawking’s earlier discussion of what makes a good theory: It should be consistent with past observations, and make testable predictions about future observations, such that it can be proven false if it doesn’t accurately describe reality. The weak anthropic principle is certainly consistent with past observations, since scientists have never observed a universe in which they cannot exist, but it makes no testable predictions, and it can’t be proven false. As such, it is more of a philosophical truism than a scientific theory.)

The strong anthropic principle (SAP) postulates that either there are an infinite number of universes, each with slightly different parameters and laws of physics, or else our universe is infinitely large, with slightly different parameters and laws of physics in each region of the universe, such that the right conditions for human life have to occur somewhere. Naturally, human observers are only present where the conditions of the universe permit them to exist.

Differentiating Between the Weak and Strong Anthropic Principles

Hawking’s original presentation of the strong and weak anthropic principles makes it challenging to distinguish between the two, because he introduces the WAP with a suggestion that the universe is “large or infinite.” This is misleading, because the WAP doesn’t really depend on the size of the universe. Instead, the WAP merely points out that you observe the part of the universe where you exist having characteristics that support your existence because if it didn’t, you wouldn’t be there to observe it.

Meanwhile, only the SAP requires that there be an infinite number of universes or places in the universe with different characteristics, such that at least one of them will inevitably support your existence. This distinction eventually comes out in Hawking’s discussion, but the way he initially defines the WAP and the SAP makes them sound almost identical.

Hawking rejects the strong anthropic principle because it doesn’t fit with the scientific method. Specifically, one of the fundamental principles of science is that the laws of physics are uniform throughout the universe. For example, if you find that a certain theory works well on earth, but not on the moon, then you need to modify the theory to work everywhere. This rules out the version of the SAP that postulates the laws of physics are different in different parts of the universe.

Meanwhile, Hawking explains that for other universes to have different laws of physics, they must be completely separate from our own: It’s impossible to send matter, energy, or information back and forth. Since you can’t possibly observe them or interact with them, whether they exist or not is irrelevant.

The SAP and the Gambler's Fallacy

Although Hawking doesn’t bring it up by name, his argument is essentially that the SAP commits a version of the “Gambler’s Fallacy.”

Imagine a game where you pay a certain amount of money to roll a die, and if you roll a six, you win the pot of money. The first time you play, you know that the odds of rolling a six are one out of six (assuming the dice aren’t loaded). Thus, on average, you’d expect to win about once every six times you play.

However, what if you’ve already played five rounds, and lost every time? Does that mean you’re guaranteed to win the next round? No, your odds of winning the next round are the same as ever: one out of six. The “Gambler’s Fallacy” is the idea that your past rolls somehow influence the probability of your next roll, such that they will average out in the end.

Similarly, Hawking argues that other universes, if they exist, are completely independent of our own. Separate universes can’t interact, and thus influence each other, just like your past rolls of the dice don’t influence your future rolls. So the existence (or non-existence) of other universes ultimately has no effect on the probability of our universe being suitable for human life.

The Inflationary Big Bang

Hawking explains that physicist Alan Guth proposed a variant of the big bang theory that would partially solve the fine-tuning problem. Guth suggested that there was a brief period of time immediately after the big-bang singularity during which out-of-balance nuclear forces acted like an anti-gravitational force, accelerating the expansion. This rapid expansion would have smoothed out any irregularities in the density of the early universe, and would also explain why the universe is expanding at just the right rate.

Guth’s idea was rooted in a principle of quantum mechanics that electromagnetic and nuclear forces become indistinguishable from each other at sufficiently high temperatures. Since the temperature of the universe would have been infinitely high at the singularity, these forces would initially have been unified. As the universe expanded and cooled off, these forces eventually separated.

However, Guth proposed that there was a slight delay between the time the temperature of the universe fell below the separation point and the time the forces actually separated, similar to how water often “supercools” before it freezes.

During this time when the forces were out of balance because the universe was “supercooled,” (cooled below the equilibrium transition temperature) they would have acted like an anti-gravitational force, accelerating the expansion of the universe. Then, when they did separate, this anti-gravitational effect would have been removed, and the expansion rate of the universe would have naturally settled down to approximately the critical rate. This would explain why the universe is expanding at just the right rate, resolving one aspect of the fine-tuning problem.

Supercooling

Guth’s argument for the inflationary big bang is rooted in the concept of supercooling, so some background on supercooling can help you understand his theory.

“Supercooling” typically means cooling a liquid below its freezing point without causing it to solidify. This is possible because when a liquid freezes, it doesn’t all solidify at once. Instead, it starts to freeze at one or more “nucleation sites,” and ice crystals (in the case of water) grow outward from these sites.

Sharp corners or particles of other solids make the best nucleation sites, particularly if the solid has a similar crystal structure to the freezing liquid. Thus, if the liquid is pure (has no solid particles of other materials in it) and is in a very smooth container, the lack of nucleation sites allows the liquid to be cooled well below its freezing point. Supercooling can lead to sudden freezing when a nucleation site eventually is provided.

This is because freezing is an “exothermic process,” meaning that you remove heat from a liquid as you freeze it. You have to remove a certain amount of heat to freeze a given amount of water (or other liquid). It takes time to transfer heat out of the liquid, so usually the liquid freezes gradually at a constant temperature, namely its freezing point.

But with supercooling, you can continue to remove heat from the liquid as its temperature drops below its freezing point. It’s like you’re storing negative heat in the liquid, so as soon as the first ice crystal forms, it grows rapidly throughout the liquid, and, if it was sufficiently supercooled, it all freezes at once.

Maybe you’ve experienced this with freezing rain. Under certain weather conditions, raindrops can become supercooled in the air, such that they freeze almost instantly when they hit the ground, forming a layer of ice over everything. Again, this instant freezing is possible because of the “negative heat” stored in the supercooled water.

Guth’s proposal relies on a similar principle, namely the “negative energy” (relative to an equilibrium state) that the universe would have stored up as it cooled beyond the point where the electromagnetic and nuclear forces separate from each other. This “negative energy” would have been stored up during the rapid, “inflationary” expansion of the universe. Furthermore, Hawking and Guth assert that negative energy density acts like anti-gravity. This means that, for a period of time, the more the universe expanded and supercooled, the more negative energy it stored up, and so the more its expansion accelerated. This caused “inflation,” or runaway expansion.

Then, when the forces started to separate (like the first ice crystal forming) it would have caused the expansion rate of the universe to suddenly “freeze up,” in the sense that the acceleration stopped abruptly, leaving it expanding at a certain controlled rate.

The No-Boundary Solution

Although the inflationary big bang theory explained why some of the initial conditions of the universe were just right, Hawking felt that further theoretical development was needed to scientifically (that is, without invoking a divine creator who could arbitrarily fine-tune the universe for the benefit of humankind) explain how the universe came to be the way it is.

This led Hawking to suggest that a quantum theory of gravity might provide a better solution, for two reasons: First, it would eliminate the “singularity” (which we’ll discuss in a moment). Second, it would address the fine-tuning problem more comprehensively. However, before we discuss these two benefits, let’s take a step back and discuss what the “singularity” is.

The Big-Bang Singularity

By the time Hawking was in graduate school, the expansion of the universe was widely accepted, and much of Hawking’s early work in physics focused on using general relativity to model the early universe.

Hawking (along with George Ellis and Roger Penrose) was able to show that, based on general relativity, the universe began at a “singularity,” that is, a point where the entire universe was compressed into an infinitely small point, with infinite density and infinite curvature of space-time. Hawking points out that at a singularity, all the laws of physics break down, because space-time itself ceases to exist. After all, if you confine space into an infinitely small space, then you don’t have any space left.

Since, as we saw in Question 1, time is relative to the curvature of space (or, equivalently, to gravity), this means that time also ceases to exist at a singularity. Thus, Hawking’s work showed that according to general relativity, time itself began at a finite point in the past.

Hawking’s mathematical proof that space and time had a beginning, according to general relativity, was what first propelled Hawking to fame within the physics community.

Did Hawking Prove the Existence of God?

Some Christians have used Hawking’s proof that time had a beginning as an argument for the existence of God and the divine creation of the universe.

Specifically, physicists sometimes define time as the dimension in which cause and effect take place, such that causes always come before the effects that they produce. If time itself came into being at some point (an effect), then there must be a cause that exists independent of the space-time of our universe to bring it into existence (cause the effect), because there is no time prior to that for a cause within our universe to trigger the big bang.

The Bible portrays God as the creator of the universe and also as being independent of the space and time that humans are confined to. Thus, the beginning of time at a singularity implies the existence of some causal agent that resembles the God of the Bible.

As we’ll see later in this Question, Hawking counters this argument by suggesting that a quantum theory of gravity will eliminate the singularity.

Eliminating the Singularity

Later, reflecting on his own theoretical proofs about the big bang singularity, Hawking came to believe that they imply the theory of general relativity is incomplete, not that the universe actually did begin at a singularity.

Hawking points out that the infinite density and temperature of the universe at the singularity are red flags, indicating a problem with the theory, because quantities are never infinite in real life. Just as quantum mechanics was developed to solve the problem that classical theories predicted infinite radiation from a hot body, a quantum theory of gravity would eliminate the singularities (and infinite quantities) that general relativity predicts.

Furthermore, according to Hawking, in quantum gravity, spacetime could take the shape of a closed four-dimensional surface (like a sphere, except that the surface of a sphere is just two-dimensional instead of four-dimensional) with no beginning or ending point. Thus, he refers to this concept as the “no-boundary model.”

Hawking explains that the “no-boundary model” makes sense because to model gravity in quantum mechanics, you have to use “imaginary numbers” for the time variable. (In mathematics, an “imaginary number” is the square root of a negative number.) According to Hawking, if you allow the time variable in a quantum model to have an “imaginary” value, then there is no longer any difference between the time dimension and the spatial dimensions of the model. This means that...

Alternative Methods of Eliminating the Singularity

Hawking is not the only physicist who thinks the big-bang singularity indicates a problem. In addition to Hawking’s “no-boundary” idea, other physicists have proposed a variety of hypothetical models that eliminate the singularity one way or another.

For example, Christoff Wetterich suggested that perhaps, instead of starting with a “big bang” in the finite past, the universe might have existed forever as a small, cold system that eventually began expanding at an accelerating rate, up until the end of the inflationary period. This has been termed the “slow thaw model”, and would be possible if the mass of all subatomic particles is gradually increasing over time. As evidence for this possibility, Wetterich cites research on the “Higgs Boson,” a subatomic particle that should theoretically have no mass, but is observed to have mass because of its interaction with a quantum energy field called the “Higgs field.’ He claims that the mass of all particles might be determined by a uniform quantum field that permeates all of spacetime, whose strength is steadily increasing over time.

Similarly, Ethan Seigel argues that the inflationary phase erased so much information that there’s no reason to assume the big bang started from a singularity. He points out that the cosmic microwave background gives us a picture of the universe right at the end of inflation, but we don’t have any data on what the universe was like before that. So, to get to the big-bang singularity, we have to extrapolate beyond our data, making arbitrary assumptions about how matter behaves under conditions we can’t observe. Thus, he doesn’t propose a single alternative model for the pre-inflation history of the universe. Instead, he points out that it could have been anything: Maybe the universe started from a singularity. Maybe it existed forever in a small volume before the period of inflation. Maybe it had a different and complex history before that. But we have no way of knowing or finding out through observation.

Finally, the “bouncing universe model” is regaining traction with some people. The bouncing universe model postulates that the universe goes through an endless cycle of expansion and contraction. Right now, it’s expanding, but it will eventually reach some maximum size and start contracting. When it gets down to a very small volume, something will cause it to rebound and the cycle of expansion and contraction will repeat itself.

The bouncing universe model was discarded by most scientists because it is hard to reconcile with the observation that the universe appears to be expanding too fast to recollapse. Although it is regaining some popularity, it is not clear how new proponents propose to address this problem.

Eliminating the Fine-Tuning Problem

Recall from the previous Question that quantum mechanics doesn’t give you an exact path for a particle that you’re modeling—rather, it gives you a probability map showing where the particle is most likely to be. You find this probability map by adding up all the possible paths that the particle could take.

Hawking conjectures that if you could model the big bang with a quantum theory of gravity, this would completely eliminate the need to fine-tune the initial conditions of the universe, because the universe wouldn’t have just one set of initial conditions, but every possible set of initial conditions. Therefore, the conditions we observe will have to show up somewhere on the probability map.

This has a similar effect to postulating an infinite number of universes, as the strong anthropic principle does, but without contradicting the scientific method as the SAP does.

Testing Hawking’s No-Boundary Theory

As we’ve discussed, Hawking says a good theory must make testable predictions. So what predictions does his no-boundary model of the universe make?

One piece of evidence that Hawking presents is that quantum effects in the early universe would have caused slight nonuniformities in the cosmic background radiation. These slight variations were observed and mapped using the cosmic background explorer (COBE) satellite in 1989. However, Hawking does not discuss whether these quantum fluctuations are unique to his no-boundary model.

Hawking concedes that, as yet, there is no complete quantum theory of gravity. Thus, his no-boundary model is really a conjecture about how future theories may allow us to resolve the issues with general-relativity-based models of the big bang, not a complete theory in itself. This limits his ability to make testable predictions based on it.

However, if space-time forms a closed surface as Hawking proposes, then one prediction it does make is that the universe will eventually stop expanding and begin contracting, since it would ultimately have to get back to where it started (just like if you travel east around the equator far enough, you’ll eventually get back to where you started).

Since the book’s publication, astronomers have determined that the expansion of the universe is actually accelerating, implying that it will probably continue to expand indefinitely and never collapse back in on itself. This doesn’t bode well for Hawking’s no-boundary model.

Answer Recap

So, how did the universe begin? According to the theory of general relativity, the universe began at a “singularity” where all matter, energy, space, and time came into existence at an infinitely small point and expanded outward from there. This concept is called the “big bang theory,” and there’s much evidence for this theory.

Exercise: Turn Problems Into Solutions

In science, new discoveries often overturn prior theories, and problems with current theories sometimes lead to new discoveries. (For example, Penzias and Wilson thought there was a problem with their microwave antenna, but eventually figured out that they had discovered the cosmic microwave background.) In this exercise, you’ll generalize this principle to consider what you can learn from problems, whether in science or in other areas of life, like work, business, or philosophy.

Briefly describe a problem or apparent contradiction that you’ve recently encountered. (For example, maybe your coworker says she emailed you an important document last week, but it never showed up in your inbox. Or maybe your houseplants suddenly start turning yellow or showing other signs of stress.)
Scientists often resolve problems by developing an improved theory, and the first step of developing a new theory is to formulate a hypothesis. List two or three hypothetical solutions to your problem.
How would you test each hypothesis you listed? That is, how will you evaluate each one to see if it would resolve the problem?

Question 4: What Is a Black Hole?

Hawking explains that a “black hole” is an object with such strong gravity that its gravity can trap light. Moreover, according to Hawking, the theory of general relativity implies that nothing can travel faster than light, so if light can’t escape from a black hole, then nothing can.

Since the black hole would trap light instead of emitting or reflecting it, it would be completely black. That said, Hawking predicts that black holes would appear to emit a small amount of radiation that’s actually produced outside the black hole, just far enough away that it can escape. To facilitate our discussion of black holes, we’ll start by introducing some terminology. Then we’ll discuss where black holes come from in the first place, after which we’ll explain “Hawking radiation,” the light that Hawking expects to be generated just outside a black hole.

Black Hole Nomenclature: Singularities and Event Horizons

General relativity predicts that there is a singularity at the center of a black hole, where all of the object’s mass is concentrated in an infinitely small, infinitely dense point. Furthermore, since there is a correlation between density and gravity, and between gravity and the curvature of space, space-time itself becomes infinitely curved at that point.

Hawking points out that the closer you get to an object, the more its gravity pulls on you. Thus, if light passes too close to a black hole, it gets pulled in. The threshold where light gets trapped forms an imaginary surface around the black hole called the “event horizon.”

Thus, Hawking notes that scientists refer to the “size” or “area” of a black hole as the size of its event horizon, which encloses a finite area, even though all the matter in a black hole is concentrated in the singularity, which is infinitely small.

(Shortform note: The diameter of a black hole’s event horizon varies anywhere from smaller than a speck of dust (for the smallest “primordial” black holes, which we’ll discuss shortly) to the size of our entire solar system, depending on the mass of the black hole. However, astronomers have not yet developed telescopes powerful enough to visually measure the size of the event horizon of any known black hole, so all black hole sizes reported to date are simply calculated based on the mass of the black hole in question.)

Where Do Black Holes Come From?

Hawking explains that most black holes form from collapsing stars. Stars, in turn, form from clouds of gas called nebulas. Eventually, gravity causes part of a nebula to collapse in on itself. As the gas gets compressed by gravity, it heats up. When it gets hot enough, it begins to undergo nuclear fusion, which releases energy (the same energy released by a hydrogen bomb). The energy released by nuclear fusion halts the gravitational collapse, and the star maintains a certain size for the stable part of its life.

Eventually, the star burns up all of its nuclear fuel. According to Hawking, when the star runs out of fuel, its gravity causes it to start contracting again. If this doesn’t trigger a supernova explosion, the star continues to contract until either nuclear forces counterbalance its gravity or it collapses into a singularity and forms a black hole. The mass of the star determines how much gravity it has, and thus determines whether or not nuclear forces can counterbalance its gravity. Stars larger than a certain size become black holes, while smaller stars become dwarf stars, because they didn’t have enough gravity to trigger the formation of a black hole.

(Shortform note: Hawking mentions supernova explosions in passing, but doesn’t really explain them. Supernovae happen because nuclear fuel is usually not distributed uniformly throughout a star, so the whole star doesn’t run out of fuel at once. Nuclear fusion doesn’t happen uniformly throughout the star either. Instead, fusion happens mostly in the core of the star, where it is denser and hotter. Sometimes, the core of a star will run out of fuel and start to collapse while there’s still plenty of hydrogen and helium closer to the surface that isn’t currently hot enough to fuse. As the star begins to collapse, the lighter elements heat up and start to undergo nuclear fusion. In some cases, this causes so many light elements to fuse at once that the sudden release of energy blows the star apart.)

Do Black Holes Actually Exist?

According to Hawking, the existence of black holes was predicted by theory and has now been confirmed by observation. He asserts that they were first hypothesized in the 1780s, based on the predictions of Newtonian mechanics.

(Shortform note: Hawking doesn’t elaborate on exactly how Newtonian mechanics predicted the possibility of black holes, but in Newtonian mechanics, “escape velocity” is the speed that an object needs in order to escape the pull of gravity (typically disregarding factors like air resistance). If you had a stellar object with such strong gravity that the escape velocity exceeded the speed of light, you would have a black hole.)

Hawking also explains that, although astronomers can’t see black holes, they can observe their effects on stars and other visible objects. He recounts that the first such observation of a black hole was in the Cygnus X-1 system, where a star orbits around an unseen object. Based on the star’s orbit, they calculate that the unseen object is about six times the mass of our sun, meaning that, as a star, it would have had enough gravity to form a black hole when it ran out of fuel.

(Shortform note: Since the publication of the book, astronomers have identified many other black holes or likely black-hole candidates.)

Black Holes Leftover From Wrinkles in Space-Time

While he says most black holes form from collapsing stars, Hawking suggests that there could be other black holes that formed shortly after the big bang due to irregularities in space-time.

(Shortform note: We infer from Hawking’s discussion of general relativity that these wrinkles in space-time would have gravity, which would attract matter to them. The more mass they accumulated, the stronger their gravity would become, until they collapsed into singularities.)

According to Hawking, theoretical calculations predict that these “primordial” black holes are relatively few and far between. At the time he wrote the book, astronomers had not identified any objects that fit the description of a primordial black hole.

(Shortform note: Scientists have not confirmed the existence of any primordial black holes since the publication of the book either. However, astronomers recently hypothesized that there could be a primordial black hole within our own solar system. Specifically, observed abnormalities in the orbits of asteroids could be explained by a black hole with an event horizon a few inches across weighing about ten times as much as the earth orbiting the sun somewhere beyond the orbit of Neptune.)

Hawking Radiation

Nothing can escape the gravity of a black hole from inside the event horizon, but radiation that’s produced just outside the event horizon can escape—and if it originates just outside the event horizon, it would appear to be coming from the black hole itself. Hawking discusses a special type of radiation produced by quantum fluctuations near the event horizon of a black hole. This radiation is known as “Hawking radiation.”

(Shortform note: Hawking published his theoretical prediction that radiation would be produced at the event horizon of a black hole in 1974, the same year he was elected a fellow of the Royal Society. “Hawking radiation'' was named after him, since it was regarded as his theoretical discovery.)

According to Hawking, the theory of quantum mechanics predicts that “empty” space is actually full of short-lived particles, or rather pairs of particles and antiparticles. Because of the uncertainty principle, there is a finite probability that a particle-antiparticle pair can spontaneously appear in empty space, and exist for a brief instant before they come back together and annihilate each other. Hawking called these particle-antiparticle pairs “virtual particles,” and refers to the event where they are spontaneously generated as a quantum fluctuation.

Hawking points out that ordinarily, virtual particles don’t last long enough to be detected. However, if a quantum fluctuation produces a photon and an antiphoton just outside the event horizon of a black hole, and the antiphoton falls into the black hole, while the photon moves away, then the photon survives indefinitely because the antiphoton can’t come back out of the black hole to annihilate it. Thus, Hawking predicts that quantum fluctuations just outside the event horizon will result in a net flow of antiphotons into a black hole and photons (particles of light) away from the black hole—meaning the black hole will have a faint glow.

Alternate Descriptions of Hawking Radiation

Particle-antiparticle pairs are only one way of visualizing quantum fluctuations. Another way is to think about them as fluctuations in the energy-density of empty space, which cannot be deterministically zero because of the uncertainty principle.

In his original scientific paper on Hawking radiation, Hawking used the energy-density approach to calculate the radiation that is produced near a black hole. However, he chose to use the particle-antiparticle description in A Brief History of Time, perhaps because it’s less mathematical and particles are easier to visualize than energy fields.

Nevertheless, some authors have criticized him for this, arguing that his original energy field description provides additional insight. For one thing, the quantum energy fields allow you to calculate the actual radiation produced, while the particle-antiparticle explanation doesn’t.

The energy field description also lets you calculate the distribution of the radiation, revealing that it’s produced in a region about fifteen times the size of the event horizon, with the intensity of the radiation highest near the event horizon, and tapering off as you get further away. Meanwhile, the particle-antiparticle description merely implies that Hawking radiation has to be produced near enough to the event horizon for the antiparticle to get trapped by the event horizon, without giving you a sense of how close it has to be for that to happen.

The Search for Hawking Radiation

To date, Hawking radiation remains largely theoretical, because it is too faint for astronomers to detect by pointing a telescope at a black hole. However, scientists have observed something analogous to Hawking radiation by simulating an event horizon in the laboratory.

Creating an actual gravitational event horizon in the laboratory is not possible at this point, but researchers were able to create a similar effect on a small scale using a block of glass and a high-powered infrared laser.

As we discussed earlier, light slows down when passing through materials such as glass. Moreover, sufficiently intense light of the right frequency can actually cause the properties of the glass to change, such that the speed of light in the glass is reduced even more. Thus, by firing a very short pulse of light at a block of glass, scientists can create a moving “speed bump” that photons are unable to get past. Since it brings photons to a standstill, relative to itself, this “speed bump” acts a lot like an event horizon.

Scientists observed photons emitted from the front of this artificial event horizon that matched Hawking’s predictions for radiation from a real event horizon.

Black Hole Thermodynamics

In addition to the predictions of quantum mechanics, Hawking argues that the concept of Hawking radiation is compelling because it would make black holes consistent with the second law of thermodynamics. For a time, scientists thought black holes might be an exception to the second law of thermodynamics, but Hawking radiation would eliminate this contradiction.

According to Hawking, the second law of thermodynamics states that the total entropy of the universe (or any other closed system) is always increasing. He explains that “entropy” is basically a measure of disorder, so the total disorder in the universe is always increasing.

While all scientists agree on the mathematical formula of the second law of thermodynamics, there is some disagreement about the best way to define “entropy” qualitatively or intuitively. Equating entropy to disorder as Hawking does is arguably the most common definition.

Another common perspective is that entropy is a measure of how difficult it is to harness or direct the energy of a system. This definition aligns the second law more closely with the first law of thermodynamics, which states that energy is always conserved. As an illustration, gasoline molecules have a lot of energy stored in their chemical bonds with relatively low entropy. When you burn the gas in an engine, its chemical energy changes into heat and mechanical energy, and its entropy increases. After you burn it, its energy is all still there (in the hot exhaust, the moving engine, and so forth) but you’ve expended its useful energy.

Hawking points out that, for a time, scientists thought black holes had no entropy because they didn’t emit radiation, and thus had no observable temperature. The higher the temperature of an object, the more thermal radiation it gives off. The entropy of an object also increases as its temperature increases. Thus, as Hawking notes, an object that emits no radiation would have no temperature and no entropy.

Hawking then describes what happens if a piece of matter that has a certain temperature, and thus a certain amount of entropy, falls into a black hole: As soon as it crosses the event horizon, we can’t observe its entropy anymore. It’s as if its entropy has been erased from the universe—which, according to the second law of thermodynamics, shouldn’t be possible because the law says entropy is always increasing, never decreasing.

However, Hawking realized that if black holes emit Hawking radiation, then they have a measurable temperature, and so their entropy can also be measured.

He came to this realization when he developed a theoretical proof that the area of the event horizon around a black hole could increase but not decrease. Hawking saw a parallel between this property of event horizons and the second law of thermodynamics, which states that total entropy cannot decrease. When Hawking published this observation, a grad student named Jacob Bekenstein suggested that maybe you could measure the entropy of a black hole by measuring the area of the event horizon.

(Shortform note: To complete the logic a bit more than Hawking does, recognize that the amount of Hawking radiation given off by a black hole would be proportional to the area of its event horizon. This is because Hawking radiation is caused by quantum fluctuations, which occur randomly distributed throughout space. So the larger the area of the event horizon, the more quantum fluctuations will occur there in a given period of time. If the amount of Hawking radiation it gives off is proportional to the area of the event horizon, and radiation is also proportional to temperature, and temperature is proportional to entropy, then the entropy of a black hole is proportional to the amount of Hawking radiation coming from it.)

Temperature, Entropy, and Black Holes

Hawking makes reference to the relationship between temperature and entropy, but he doesn’t explain this relationship in detail. Let’s back up and discuss this relationship so we can show how it ties into Hawking’s discussion of black holes. The exact relationship between temperature and entropy is defined by the second and third laws of thermodynamics.

Specifically, part of the second law states that the change in entropy of a substance or system is equal to the thermal energy that is transferred to it, divided by its absolute temperature. For example, it takes about 333 joules (J) of energy to melt a gram of ice, and ice melts at zero degrees celsius, or 273 kelvin (K), so melting a gram of ice increases its entropy by 333 J / 273 K, or about 1.22 J/K.

However, the second law only defines the change in entropy for thermodynamic processes. The third law defines absolute entropy, by establishing that the entropy of a pure element or compound is zero when its temperature is absolute zero (zero kelvin) and it is in the form of a perfect crystal. If the substance has impurities or irregularities in its crystal structure, such that its molecular structure is more disordered, then it retains a small amount of entropy, even at absolute zero.

So, if you want to calculate the absolute entropy of something, you use this as a starting point, and then you calculate the change in entropy to get it to its current state and temperature. For example, the heat capacity of a gram of ice is about 2.093 J/K, so it takes about 571 J to warm a 1g ice crystal from 0 to 273k. The average temperature during this process would be 273/2 K, so the change in entropy would be about 4.18 J/K. When it melts, that adds another 1.22 J/K, so the absolute entropy of a gram of water at 273 K is about 5.4 J/K.

You can find the total entropy of a system by adding up the entropy of its parts. So, if a gram of water with a temperature of 273 K falls into a black hole, the entropy of the black hole must increase by 5.4 J/K, according to the laws of thermodynamics. The additional mass of the water increases the mass of the black hole, which increases its gravity, which in turn increases the size of its event horizon. The larger event horizon produces more Hawking radiation, so, theoretically, you can measure the increase in the black hole’s entropy by the increase in Hawking radiation when the water falls in.

Answer Recap

So, what is a black hole? Basically, a black hole is a star that runs out of nuclear fuel and succumbs to a runaway gravitational collapse, such that it collapses into a “singularity,” where all its mass is confined to an infinitely small point. There’s a finite area around the singularity where its gravity is so strong that it can capture light. The boundary of this area is called the “event horizon” because you can’t observe any event that happens inside it, since light from the event can’t reach you.

Theoretically, quantum fluctuations just outside the event horizon give black holes a faint glow. This is called “Hawking radiation.”

Question 5: Can You Build a Time Machine?

Writers of science fiction have long contemplated the idea of a time machine: a device that allows you to travel forward or backward in time to any point in history or the future. Hawking asserts that this possibility will probably always be relegated to the realm of fiction, based on his analysis of relevant scientific theories. His analysis focuses on two possibilities: moving backwards through time directly, or passing through a “wormhole” in spacetime that connects the present to the past.

Moving Backwards Through Time

Hawking begins his analysis of time travel by observing that time is reversible in all the laws and theories of physics. The math would be just as valid if time was running backwards as it is when time is running forwards. And yet, you never observe time running backwards (except in a certain interpretation of quantum fluctuations, which we’ll discuss later). To explain why we perceive time moving forwards and not backwards, Hawking first provides three ways to define the direction of time and shows how they relate to each other. This sets the stage for his assessment of the possibility of backwards time travel based on relativity and quantum mechanics.

(Shortform note: Reverse time simulations are widely used in some fields, such as forensic science. For example, if you know where each of the vehicles involved in a traffic accident ended up after the collision (and if you have enough information about physical parameters like coefficients of friction), you can use the laws of physics to extrapolate backwards in time and reconstruct the collision. Investigators sometimes use reverse-time computer simulations like this to aid in determining who was at fault in the accident.)

Defining Which Way Time Moves

You probably have an intuitive idea of what it means to move backwards versus forwards in time, but how do you formally define the direction of time? Hawking defines three “arrows of time,” providing three different ways to distinguish between going forward and backward in time:

The thermodynamic arrow of time is based on the second law of thermodynamics, which states that the total entropy of the universe (or any closed system) cannot decrease. (Recall that entropy is a measure of disorder.) Thus, time moves forward in the direction that the entropy of the universe increases.
Hawking defines the psychological arrow of time as the direction that humans perceive time progressing: You remember the past and have to wait and see what the future will bring.
Hawking defines the cosmological arrow of time based on the expansion of the universe: Time moves forward as the universe expands and backward as it contracts.

Additional Arrows of Time

Others have proposed a number of additional arrows of time besides the three that Hawking defines:

The Radiation Arrow is based on how waves travel. Specifically, waves (like light or sound) always radiate away from their source. So time moves forward as waves radiate outward, and backward as waves converge toward their source.

The Cause-and-Effect Arrow is defined by the principle that when one event causes another, the cause always comes before the effect.

The Nuclear Arrow is defined based on the decay rates of subatomic particles. Specifically, some unstable particles have slightly different decay rates than their corresponding antiparticles. This difference can serve as a reference to mark the direction in which time progresses.

Time in Thermodynamics and Human Perception

Hawking argues that the psychological arrow of time necessarily points the same way as the thermodynamic arrow because the human brain obeys the second law of thermodynamics.

Drawing an analogy between human memory and computer memory, he points out that the process of storing information in computer memory generates entropy, and asserts that human learning also generates entropy. Since storing memories in your brain increases the entropy of the universe, your memories all point back to times when the entropy of the universe was lower.

(Shortform note: In A Mind for Numbers, Barbara Oakley explains that the neurological processes involved in learning and remembering information generate toxins that are flushed out of your brain every night while you sleep. Oakley uses this to illustrate the importance of sleep for learning, but these toxins could also be used as a measure of the amount of entropy generated in the learning process, since they are high-entropy molecules that are periodically purged from the system.)

Time in Cosmology

Hawking reports that when he formulated the first version of his “no-boundary” model of cosmology, he thought that the cosmological arrow of time would also point the same direction as the thermodynamic and psychological arrows. Thus, when the universe stopped expanding and started contracting, its history would replay in reverse. Any people alive during the contraction phase would remember the future instead of the past, since entropy would be decreasing.

However, as Hawking refined his model, he realized that this concept was wrong. Actually, the entropy of the universe would continue to increase during the contracting phase as well, so the thermodynamic and psychological arrows of time would continue to point the same way as during cosmic expansion. If you lived during the contracting phase, you would still remember the past and not the future.

That said, Hawking also notes that humans will not be around during the contracting phase, because current models predict the universe will succumb to a “heat death” before the universe stops expanding and begins contracting. A “heat death” basically means a state where all energy sources have been exhausted, to the point where it is no longer possible for complex lifeforms to survive.

The Cosmological Time Debate

Physicist Richard Muller would probably disagree with Hawking’s conclusion that time would continue to move forward in a contracting universe, since Muller argues that the expansion of the universe is what fundamentally defines the arrow of time.

According to Muller, this is because time is growing, just like space. Muller points out that, according to general relativity, the universe is not merely expanding in space, but rather space itself is expanding. It has been expanding ever since the big bang, when it came into being at a singularity. And it isn’t just space that’s expanding: As spacetime expands, time is expanding along with space. The expansion of the time dimension manifests itself as the progression of time.

Muller dismisses the thermodynamic arrow of time. If increasing entropy defined the progression of time, then traveling back in time would be as easy as reducing the entropy around you. But this is not what we observe. Muller concedes that the total entropy of the universe increases as time progresses, but points out that the local entropy of regions within the universe can increase or decrease at any time. (As we discussed earlier, to store information in memory, you have to decrease the entropy of the memory chip, albeit by creating more entropy elsewhere.)

Muller doesn’t specifically discuss how time would be different in a contracting universe, probably because it is now widely accepted that the expansion of the universe is accelerating, and so it’s not expected to ever contract. However, we can infer from his definition of time that if spacetime stopped expanding and started contracting, the direction of time would reverse.

Time Travel in General Relativity

However, he also points out that, based on the theory of relativity, nothing can travel faster than light. This is because mass is also related to speed, so that it takes an infinite amount of energy to accelerate anything that has mass to the speed of light, let alone beyond it (as we discussed in Question 1). Since all people and machines are made of matter that has mass, this precludes going back in time by exceeding the speed of light.

Using Time Dilation for Pseudo-Backwards Time Travel

As we discussed in Question 1, Hawking explains how space and time are relative to the observer, so you may perceive time and distance passing differently than someone else does. When he discusses the possibility of backwards time travel, he concludes that literally going back in time is unlikely to be possible, However, he doesn’t explicitly discuss the possibility of going back in time relative to someone else, which is clearly possible based on his explanation of relativity.

To illustrate this, imagine that you and your sister have both signed up to emigrate to a new colony on a planet that’s a thousand light-years away from earth. Before you leave, let’s say your sister is two years older than you. The two of you board different starships to travel to the colony and blast off at the same time.

Your sister’s ship makes the trip at a speed of 99.99995 percent of the speed of light, so from her perspective, the trip takes one year, while observers on earth see it taking her 1000 years and four hours to make the trip.

Meanwhile, your ship makes the trip at a speed of 99.9992 percent of the speed of light, so from your perspective, the trip takes four years, while observers on earth see you taking 1000 years and three days to make the trip.

You and your sister left at the same time and arrived within a few days of each other, but during the trip, you aged four years while your sister only aged one year, so now your sister is a year younger than you instead of two years older. The effect on your relative age is the same as if you’d gone backward in time three years. So, in a sense, you could say you’ve traveled backwards in time relative to your sister.

Time Travel in Quantum Mechanics

He explains how this principle provides an alternate way to visualize quantum fluctuations. Instead of picturing a quantum fluctuation as a particle-antiparticle pair that spontaneously appears for an instant before the particle and its antiparticle come back together and annihilate one another, you can think of it as a single particle moving in a closed loop through spacetime. For half of the loop, the particle is moving forward in time, and for the other half it is moving backwards in time. The backward part of the loop is equivalent to the anti-particle moving forward to collide with the particle.

By the same token, Hawking explains that you can picture Hawking radiation as an anti-photon that travels backward in time as it moves from the center of a black hole out to the event horizon (moving backward in time is the only way it could escape from the center of the black hole out to the event horizon). Then, at the event horizon, the anti-photon that’s traveling backwards through time morphs into a photon that’s traveling forward through time, and it continues on its path away from the black hole. (Now that it’s outside the event horizon, it can escape the black hole’s gravity.)

However, as we’ve discussed, Hawking also points out that quantum mechanics only accurately describes the behavior of very small particles, so the possibility of backwards time travel for quantum particles doesn’t seem to apply to people or macroscopic objects.

Psychological Perception of Quantum Time Travel

As Hawking points out, scientists are not aware of any way to use quantum time travel to send humans back in time. However, another potential problem with quantum time travel comes up if you consider it in light of Hawking’s earlier discussion of the psychological arrow of time.

Specifically, even if you could move backward through time like a quantum particle, presumably that wouldn’t change how thermodynamics works in your body and brain. So, you’d still only be able to remember the past, that is, the state of the universe when it had less entropy. Thus, traveling backwards in time would erase your memory back to the time you returned to.

The rest of your body obeys the laws of thermodynamics as well, so if you could move backwards in time, your physical age would decrease. If you tried to go back to a time before you were born, you would probably cease to exist.

Hawking himself doesn’t explore this aspect of time travel, but it seems like something we can infer from his discussion of the thermodynamic and psychological arrows of time.

Wormhole Time Travel

Hawking reports that in 1935, Albert Einstein and Nathan Rosen showed that the theory of general relativity predicts that it’s possible for a bridge to form between warped regions of spacetime, potentially creating an alternate pathway between points in time and space. Initially, these hypothetical pathways were called “Einstein-Rosen Bridges,” but have since been renamed “wormholes.”

According to Hawking, wormholes might be your best bet for traveling back in time, because, hypothetically, you could travel forward in time as you go through the wormhole, but arrive at a point in the past when you come out the other end. However, he cautions that this possibility is still extremely unlikely in practice.

Wormholes Aren’t Stable

For one thing, Hawking asserts that general relativity predicts wormholes would be extremely unstable. If any mass (such as a person or a vehicle) entered the wormhole, its gravity would affect the curvature of spacetime enough to cause the wormhole to collapse. So even if you could find a wormhole to the past, if you tried to go through it, chances are that neither you nor the wormhole would survive.

(Shortform note: There are ongoing hypothetical studies of wormhole stability. Recently, one team showed that, in their model, it would be possible for tiny particles like photons and electrons to pass through a microscopic wormhole without causing it to collapse. However, their model itself is still under development and has yet to be tested against observations of the real world. Their model combines elements of quantum mechanics, general relativity, and classical electrodynamics.)

Wormholes Require Negative Energy

For another thing, Hawking explains that wormholes require spacetime to have concave curvature.

But the only curvature that scientists have ever observed is convex. The presence of a massive body causes convex curvature of space, resulting in gravity. Hawking asserts that convex curvature also correlates to a positive energy density, but concave curvature would require space to have a negative energy density.

(Shortform note: The reason convex curvature corresponds to positive energy density is that, according to the theory of relativity, mass is interchangeable with energy, as expressed in the famous equation E=mc². This means that mass is basically a form of energy, and therefore, the presence of mass implies the presence of energy.)

Hawking notes that negative energy fields are possible in quantum mechanics, provided they are balanced out by positive energy fields. However, he adds the caveat that it’s hard to say whether this principle would apply to the kind of fields that warp spacetime on a large scale, because there is not yet a quantum theory of gravity.

(Shortform note: Recall that, according to general relativity, gravity is the curvature of space, so you would need a quantum theory of gravity to determine if quantum energy fields could produce the right kind of spatial curvature.)

Answer Recap

So, can you build a time machine? Not easily.

If you could go faster than light, time would run backwards for you, relative to other observers. But according to general relativity, it’s impossible for you to go faster than light.

According to quantum mechanics, subatomic particles can travel backwards in time, but Hawking doesn’t suggest any way you could use this principle to make macroscopic objects travel back in time.
Theoretically, it’s possible to have a “wormhole” that connects two different regions of spacetime. Thus, Hawking views wormholes as the best possibility for time travel. However, he also points out that wormholes require a type of space-time curvature that scientists have never seen happen in the real world. He also conjectures that, if you could create a wormhole, it would probably collapse as soon as you tried to go through it.

Exercise: Consider Your Approach to Time Travel

Hawking views time travel (at least backwards or arbitrary time travel) as unlikely, but he discusses how quantum particles can travel back in time and how wormholes could connect two different points in spacetime that might be located in different time periods.

As technology progresses, do you think developing time travel is technically feasible? Why or why not?
Assuming it’s technically possible to develop time travel technology, do you think humans should invest resources in developing it? Why or why not?
Suppose a company succeeded in creating a wormhole that takes you one week backwards (or forwards, if you prefer) in time. They’ve demonstrated that traversing the wormhole is reasonably safe, and the cost of a ticket to last week costs about a week’s wages. Would you ever use this technology? If so, what would you use it for? If not, why not?
Now imagine that today you accidentally fall into a temporary wormhole created by a glitch in the one-week-wormhole device, and you suddenly find yourself transported one week backward in time. As soon as you arrive, the wormhole implodes, so you can’t go back through it. Now that you’re compelled to relive last week, what would you do differently?

Exercise: Use Science to Write Science Fiction

Imagine that the writers of a new science fiction series have hired you as a consultant. They want their series to be reasonably scientifically accurate.

Season 1 of the series is about people leaving earth and traveling to a distant planet to build a new colony. They’ll make the trip on spaceships that travel very close to the speed of light. Brainstorm a few ideas for interpersonal drama or other plot elements that could arise from the relativity of space, time, or motion, as people travel to the new colony. (For example, because the ships are traveling close to the speed of light, the people on board will age much slower than their loved ones back home, which could cause problems.)
Season 2 of the series centers around a computer-genius character who claims to have developed a mathematical model of the colony so detailed that his computer program can predict the future. Thinking back to our discussion of quantum uncertainty and the challenges of unifying quantum mechanics with general relativity, brainstorm a few ideas for episodes or plot twists that the writers could use in Season 2.
In Season 3 of the series, a red giant star about five light-years away from the colony collapses into a black hole and the colonists send a scientific expedition to study the black hole. The writers want to cover both drama on the expedition and back on the colony while the expedition is underway. Brainstorm a few ideas for episodes or plot elements to use in Season 3.
Season 4 of the series focuses on time travel. However, before the writers can flesh out the episodes, they need to agree on how time travel works in their series. What mechanism of time travel would you advise them to use? (For example, maybe the colonists find a way to manipulate the gravity of the black hole that formed in the previous season such that they can create a wormhole, and they try to create a wormhole back to Earth for ease of future communications. Maybe they succeed in creating the wormhole, but the other end forms in the Bermuda triangle in the 1800s, or some other historical time period, and the wormhole collapses as soon as they send a team through it, so they can’t immediately get back.)
Given your answer to the previous question, brainstorm a couple of ideas for episode plots or plot twists to use in Season 4.