How to Lie With Statistics

1-Page Summary

When searching for the truth, statistics are appealing—they seem like hard, believable numbers, and they’re necessary for expressing certain information, such as census data.

However, statistics aren’t as objective as they seem. In How to Lie With Statistics, author Darrell Huff explains how people who want to conceal the truth manipulate numbers to come up with statistics that support their positions. These people—advertisers, companies, anyone with an agenda—often don’t even have to actually lie. Statistics is a flexible enough field that would-be liars can make their case with implications, omissions, and distraction, rather than outright falsehoods.

Not all bad statistics are manipulations or lies, of course. Some are produced by incompetent statisticians; others are accidentally misreported by media who don’t understand the field. However, because most mistakes are usually in favor of whoever’s citing the statistic, it’s fair to assume that a lot of bad statistics are created on purpose.

In this summary, you’ll learn the techniques shady characters use to lie (or imply) with statistics. You’ll also get a five-step questionnaire for evaluating the legitimacy of statistics you come across.

Technique #1: Misleading With Bad Sampling

To get their numbers, honest statisticians count a sample of whatever they’re studying instead of the whole (counting the whole would be too expensive and impractical) and take steps to make sure the sample’s make-up accurately represents the whole. They do this by making sure the sample is large (this reduces the effects of chance, which only has a negligible impact on large samples) and random (every entity in the group must have an equal chance of being part of the sample).

On the other hand, liars purposely take samples that don’t accurately represent the whole to engineer the results that they want. Or, they take small samples so that chance gives them the results they want.

For example, if a liar wants to say that her toothpaste reduces cavities, she might ask 12 people with healthy teeth (as opposed to a group of people with a variety of dental health levels) to start using it. If this group of 12 doesn’t show any reduction in cavities, she can try the same experiment with another group of 12. Since the only possible outcomes of using toothpaste are getting more cavities, fewer cavities, or the same number of cavities, eventually the 12-person sample will by chance all (or mostly) hit on a reduction in cavities. This is much less likely to happen in a sample of, say, 120 people.

Techniques #2-6: Fudging the Numbers (or the Point)

Technique #2: Citing Misleading “Averages”

Liars often use the word “average” without specifying what kind of average a figure represents. For instance, they may use it to refer to mean—the number that’s the result of adding up all the sample’s numbers and then dividing by the number of samples.

(Shortform example: To get the mean income of five people, you’d add up all their incomes and divide by five: 30,000+30,000+50,000+60,000+70,000=48,000.)

Giving the mean is advantageous for liars because it hides large inequalities.

(Shortform example: If 90 employees at a company are paid $20,000 a year and the boss is paid $200,000, the mean pay is ((9020,000)+(1200,000))/91=21,978. The mean hides that one person is paid a lot more than everyone else.)

In turn, hiding that they’re using the mean, by simply using the word “average” to describe the figure, benefits liars by obscuring the fact that they’re using such an unreliable calculation.

Technique #3: Giving Precise Figures to Appear More Reputable

Another number-fudging technique is to include a decimal in a statistic to make a figure look more precise and therefore reputable. Liars can engineer decimals by doing calculations (for example, calculating the mean) on inexact figures that weren't measured to the decimal point.

(Shortform example: If you ask 100 people how much they spent on groceries in the last month, they probably won’t remember exactly. Even if they give you round, approximate numbers, if you calculate the mean, you’ll likely end up with a decimal. For instance, (20+30+60)/3=36.66666... This number is meaninglessly more precise than the measures you started with, but it looks good.)

Technique #4: Using Percentages to Hide Numbers and Calculations

Like decimals, giving percentages instead of raw figures can make numbers look more precise and reputable than they really are. (Shortform example: If two out of three people prefer a certain cleaning product, this can be expressed as 33.333…%. The decimal adds precision and implies reputability.)

Here are some additional ways liars manipulate percentages and their associated terms for their gain:

1. Hiding raw numbers and small sample sizes. Percentages don’t give any indication of the absolute value of raw figures, so liars can use them to mask unfavorable numbers or suspiciously small sample sizes.

(Shortform example: If a stock was worth $1 yesterday and $2 today, that’s a 100% increase, which looks impressive. However, the actual difference is only $1, which looks unimpressive.)

2. Using different bases. Because percentages don’t give any indication of the raw figures (bases) used to calculate them, liars can compare percentages calculated off different bases to distort their results.

For example, The New York Times once reported that after taking a 20% cut last year, union workers got a 5% raise the next year, which gave them back one-fourth of their cut wage. This claim of it being one-fourth of their cut wage refers to 5% being one-fourth of 20%. However, the workers didn’t actually get 5% of their original wage back, they got a 5% increase on their new, lower wage, which is a smaller number. The 20% cut and the 5% increase were calculated off different bases, so weren’t directly comparable.

3. Adding up percentages. Percentages aren’t numbers—you can't meaningfully add or subtract them.

For example, imagine you buy 20 vegetables at the grocery store and all of them cost you 5% more than they did last year. If you add together all of those 5% increases, you get a 100% increase (20*5%=100%). This could be reported as “the cost of living has gone up by 100%.” But in reality, it hasn’t—it’s gone up by 5%, and all products were affected.

4. Giving percentage points instead of percentages to confuse people. Percentage points are the difference between two percentages. For instance, the difference between 5% and 7% is two percentage points. If a liar doesn’t want to report how much money her company made, and her return on investment was 3% last year and 6% this year, she might say “return on investment rose three percentage points.” A three-point increase sounds much smaller than a doubling, even though they mean the same thing in this case.

Technique #5: Omitting Statistical Qualifiers

The last way to fudge numbers is to leave out information that puts caveats on their accuracy or further explains them. There are four types of information liars often neglect to include with their figures:

1. Probable error. Probable error is a measure of how reliable a figure is, expressed as a range that the true result will fall between. (It’s impossible to find the single number that represents the true result because measuring systems aren’t perfectly accurate.) Therefore, if you’re presented with a single figure, and aren’t given any indication of how accurate it is, it may not be accurate at all.

For example, if an IQ test has a probable error of 3 and you score 98, this means that your IQ is somewhere between 95-101 (98-3=95, and 98+3=101). The real number is equally likely to be any number in that range. So, simply telling someone that your IQ is 98 isn’t accurate.

2. Degree of significance. The degree of significance is a measure of how likely it is that results are due to chance. In most cases, for a figure to be statistically significant, the degree needs to be no more than 5%—this means that 95 out of 100 times, the results are real and not attributable to chance. If the degree isn’t given, it may be higher than 5%, which means the results could be due more to chance than anything else.

3. What the comparison is to. Some stats promise to “triple” the effectiveness of a product, or offer “25% more,” but don’t say what they’re compared against. A granola bar that contains 25% more protein than a competitor’s, versus a bar that contains 25% more protein than a rock, are two entirely different things.

4. Negligibility. While there may be mathematical differences between figures, sometimes, these differences are so small they don’t make any practical difference—but liars fail to point this out.

For example, one brand of cigarette may contain a slightly smaller amount of poisonous compounds than another. It’s still toxic.

If liars can’t find a calculation that gives them figures they like, another technique they use is to focus on other figures that do seem to support what they have to say: in other words, to fudge the point. If they can’t prove something, sometimes, they’ll prove something else that sounds like it's the same as what they were trying to prove.

For example, if a cold medicine company can’t prove that their drug cures colds, but they can prove that it kills germs in a lab, they might advertise that their medicine “kills 15,000 germs.” Killing germs isn’t the same as curing colds (colds probably aren’t even caused by germs), but they’re close enough that people might think the medicine actually works.

Technique #7: Attributing Correlation to Causation

This technique involves pushing the idea that if there’s a relationship between two factors, one of them caused the other, and whichever factor is most favorable to a liar’s argument is the cause.

For example, one study found that smokers got lower grades in college. A non-smoking activist with an agenda might report this as “If you stop smoking, your grades will improve.”

This is misleading because:

1. It’s often impossible to know which factor is the cause and which is the effect.

For example, people struggling with the stress of bad grades could be driven to smoking for relief: In other words, bad grades could be the cause of smoking, not the effect of it.

2. Both factors may be effects of some other cause. While the relationship between the factors is real, the cause-and-effect is uncertain.

For example, maybe the same people who smoke are the same people who have low grades because they like socializing more than studying.

3. The relationship between the two factors may be only due to chance.

4. Even if there is a real cause-and-effect relationship, that doesn’t mean it applies to everyone. Correlations are tendencies.

For example, while it’s fairly conclusive that people who get a post-secondary education have higher incomes than those who don’t, that doesn’t mean that you will make more money if you go to college than if you don’t.

5. Correlations can be caused by humans and trends, rather than the factor you think they’re caused by.

For example, older women tend to walk with their toes farther apart than younger women. This is because posture trends changed over the years, not because women’s posture necessarily changes as they age (which is what some people may assume).

Techniques #8-10: Manipulating Images

Technique #8: Truncating Graphs or Add More Divisions to the Y-Axis

To make changes look larger than they are, liars remove the empty space on a graph so that the part the data occupies is the only part shown. This will make the slope of a line look steeper, or the difference between bars look greater.

For example, from this graph, it’s obvious that there’s little difference in profit from year-to-year:

In this graph, which uses the same data as the first graph but has more divisions and has been truncated, profit looks significantly different from year to year:

Technique #9: Failing to Include Labels and Numbers on Graphs

If diagrams and graphs don’t have labels or numbers, it’s impossible to know what they show.

For example, one advertising agency presented a graph that showed a steadily rising line. The y-axis showed time in years, but the x-axis had no label. Presumably, it was profit, but without further labeling, it was impossible to know if profits were jumping by millions or cents.

Technique #10: In Bar Graphs, Using Illustrations Instead of Bars

In a bar chart, the height of the bar is what indicates the measurement. If you replace a bar with an illustration, when you increase the height of the illustration, all the other dimensions scale proportionally. Increasing the width and depth (if 3-D) of the image makes the differences between the two images—and thus the differences between what the images represent—look much larger than they really are.

(Shortform example: In the illustration below, the skulls represent the death rate from a certain illness. Before a liar’s medication was adopted, the death rate was 60 out of 1 million, represented by a skull at height 60. After adoption, the death rate halved to 30, represented by a skull at height 30. However, visually, the rate appears to have dropped by far more than half because the image appears to have decreased by more than half: The whole image was scaled proportionally, rather than just the height being halved.) Death rate pre-adoption:💀Death rate post-adoption:💀

Assessing the Legitimacy of Statistics

In the previous sections, you learned liars’ techniques for misrepresenting statistics. Now, you’ll learn about a five-question checklist you can go through every time you encounter a statistic to assess its legitimacy. The goal is to find balance—you don’t want to swallow statistics without thinking about them (it’s often worse to know something wrong than to be ignorant), but you also don’t want to be so suspicious that you ignore all statistics and miss out on important information.

Here are the evaluation questions:

1. What is the source of the statistic? The first thing to do when confronted with a statistic is to figure out where it’s coming from. If the source might have an agenda, you should be suspicious of the statistic. (Note that liars often borrow the numbers of reputable organizations, such as universities or labs, but come to their own conclusions using those numbers. Then, then try to make it look like their conclusion is the reputable organization's conclusion, to give their conclusion more credibility. Check if the organization that provided the numbers is the same one that provided the conclusions drawn from them.)

2. What was the data collection method? Any data that’s based on what respondents say, or how motivated they are to respond to a survey, can skew the truth. When confronted with a statistic that was calculated based on people’s responses, ask yourself if there were any reasons the respondents might have been motivated to lie.

For example, one census in China, for military and tax purposes, found the population of one region to be 28 million. The next census, for famine relief purposes, found the population of the same region to be 105 million. The population hadn’t changed much over the five years in between censuses—people were just a lot keener to be counted when it meant famine relief than when it meant getting taxed.

3. Is any relevant information omitted? Figures exist in context. If a figure is cited on its own, ask yourself if there is other relevant information that might qualify the figure further, and if leaving that information out would further anyone’s interests.

For example, an environmentalist who wants the government to regulate pollution might cite a high death rate during pollution-driven foggy weather in London and attribute the deaths to the fog. However, this doesn’t represent how the world works—people die for plenty of reasons that don’t have anything to do with the weather, and the high death rate could have been caused by something else. A more accurate statistic would be to cite the death rate accompanied by the cause of death: This would show how many people truly died due to fog.

4. Is the language surrounding the figures misleading? Study the words surrounding the figure and consider their definitions (to twist their results to suit their argument, liars may not use the most common definition of an everyday word, as you learned with “average”).

(Shortform example: Anything can be the “first,” “biggest,” or “best” of its kind, depending on how people define these words. For instance, the “biggest” waterfall in Canada is Niagara Falls (if “big” means the largest volume of water falling) or Della Falls (if “big” means highest).)

5. Does the statistic make sense? Ask yourself if whatever the statistic reveals seems right, if it conflicts with any well-known facts, or if it’s suspiciously precise.

For example, one urologist calculated that there are eight million cases of prostate cancer in the US. At the time, the male population of the US was less than eight million, which meant the figure couldn’t be accurate.

Chapter 1: Misleading With Bad Sampling

When searching for the truth, statistics are appealing—they seem like hard, believable numbers, and they’re necessary for expressing certain information, such as census data. Many people take statistics at face value because they suspend their common sense when presented with numbers, panic at the thought of complicated calculations, or feel math can’t lie.

Not all bad statistics are manipulations or lies, of course. Some are produced by incompetent statisticians; others are accidentally misreported by media who don’t understand the field. However, because most mistakes are usually in favor of whoever’s citing the statistic, it’s fair to assume that a lot of bad statistics are created on purpose.

In the first four chapters of this summary, you’ll learn the techniques shady characters use to lie (or imply) with statistics. In the last chapter, you’ll learn a five-step checklist you can use to spot liars’ techniques in the wild.

(Shortform note: We’ve rearranged the original book’s content for concision and clarity.)

In this chapter, you’ll learn about sampling—the pool from which statisticians get their numbers. First, we’ll look at how sampling is supposed to work. Then, we’ll look at how liars deliberately manipulate sampling to further their ends.

Good Sampling

The only way to get a perfectly accurate statistic is to count every entity that makes up the whole. For example, if you want to know how many red beans there are in a jar of red-and-white colored beans, the only way to find out for sure is to count all of the red beans in the jar.

However, in most cases, counting every single entity is impossibly expensive and impractical. For instance, imagine you were trying to know how many red beans there are in every jar on the planet—you’d have to count all the red beans in the world at any given time.

To get around this problem, statisticians count a sample instead of the whole, assuming the sample’s make-up proportionally represents the whole.

A sample must meet the following two criteria to actually be representative of the whole (and thus, be “good”):

Criteria #1: Large. This reduces the effects of chance—chance affects every survey, poll, and experiment, but when the sample size is large, its effects are negligible.

For example, the probability of getting heads when flipping a coin is 50%. In practice, if you flip a coin 10 times, you’re unlikely to get heads five times. You’ll probably get some other number due to chance—say, three. If you don’t flip the coin any more times, you’re left with the impression that the probability of getting heads is 3/10, or 30%, which is clearly incorrect. You’ll need to flip the coin 1,000 times to reduce the effects of chance and get a figure closer to the real probability of a half.

How big your sample needs to be depends on what you’re studying. For example, if the incidence of polio is one in 500, and you want to test a vaccine, you’ll have to vaccinate far more than 500 people to get any meaningful results about the vaccine’s efficacy. It's hard to know if the vaccine works if, even without its use, only one person would have contracted the disease anyway.

Criteria #2: Random. Every entity in the complete group must have an equal chance of being selected to be part of the sample. Perfectly random sampling is too expensive and unwieldy to be practical. (Even if you were only going to randomly select one bean in 1,000 to be part of the sample, you’d first need a list of every bean in the world to even determine where to find each thousandth bean.) Instead, statisticians use stratified random sampling, which works like this:

Statisticians divide the whole into groups: for example, people over the age of forty, people under the age of forty, Black people, white people, and so on.
They select samples from each group. How many are taken from each group depends on the group’s proportion in relation to the whole.

Despite statisticians’ best efforts, bias is always present when choosing samples because:

Statisticians might get the proportions wrong and over or under-represent certain groups.
Statisticians can’t always tell which entity belongs to which group. (Shortform example: You might be able to tell how many people have red hair by looking at them, but how do you know if it’s naturally red?)
When sampling people, interviewers may be biased in their choice of subjects. (For example, if an interviewer has the choice between two people from the same group, she might choose the one who looks friendlier, to make it easier to get her job done.)
Interviewers might bias respondents. For example, one wartime poll asked Black people living in the South what they thought was more important, beating the Nazis, or bolstering democracy in the US. The Black interviewers found 39% of respondents prioritized beating the Nazis, while white interviewers found 62%. Black people might be more inclined to give white interviewers the answer they think they want, rather than tell them what they actually believe, so that they appear more loyal.

Bad Sampling

Now we've looked at what makes good sampling, let’s look at the opposite—bad sampling. There are two ways liars manipulate sampling to skew statistics:

1. They use a small sample size. Because chance affects small samples more than large ones, liars might sample just a few entities so that they can use chance to their advantage. If they don’t get the result they want, they can keep experimenting until chance gives them the numbers they do want.

For example, if a liar wants to say that her toothpaste reduces cavities, she might ask 12 people to start using it. If this group of 12 doesn’t show any reduction in cavities, she can try the same experiment with another group of 12. Since the only possible outcomes of using toothpaste (and being alive) are getting more cavities, fewer cavities, or the same amount, eventually the 12-person sample will by chance hit on a reduction in cavities.

2. They purposefully bias the sampling. If a liar wants a particular result, she’ll sample the parts of the whole most likely to give them that result.

(Shortform example: If you want to show that most of your friends believe the world is flat, you might sample five of your Facebook friends. To get the result you want, you’d ask five people who belong to flat-earth Facebook groups, rather than five random friends.)

Chapter 2: Fudging the Numbers

In the last chapter, you learned how people manipulate samples to get favorable stats. Now, you’ll learn how liars pull or imply favorable numbers from existing data, without even having to change anything about the sample.

There are five techniques for fudging numbers:

Technique #1: Citing Misleading “Averages”

The first technique is using the word “average” without specifying what kind of average a figure represents. Each kind is calculated differently and gives different information (and a different impression) about the data:

Average Type #1: Mean. This number is the result of adding up all the sample’s numbers and then dividing by the number of samples.

(Shortform example: To get the mean income of five people, you’d add up all their incomes and divide by five: ($30,000+$50,000+$70,000+$70,000+$70,000)/5=$58,000)

This is a useful average for liars to use because it allows them to:

Make the number look bigger and better. (Shortform example: If a university wants to attract students, the larger the average income of its graduates, the more attractive it looks to prospective students. Even if there are just a few high salaries, the math will make the mean look higher than any of the other averages.)
Hide inequality. (Shortform example: If 90 employees at a company are paid $20,000 a year and the boss is paid $200,000, the mean is ((9020,000)+(1200,000))/91=21,978. The mean doesn’t show that one person is paid a lot more than everyone else.)

In turn, hiding that they’re using the mean, by simply using the more general “average” to describe the figure, benefits liars by obscuring the fact that they’re using such an unreliable calculation.

Average Type #2: Median. This is the number that falls in the middle when the sample numbers are arranged in numerical order. The median is a useful number for you as a seeker of the truth because it gives you information about the data distribution—half of the sample numbers are above the median and half are below.

(Shortform example: The median of the five people who make $30,000, $50,000, $70,000, $80,000,and $80,000 is $70,000.)

Average Type #3: Mode. This is the number that appears most frequently in a data set.

(Shortform example: The mode of the above list is $80,000.)

When the distribution of a data set is normal (most of the values fall in the middle, with just a few on the extremes), all of the averages will be similar. However, when the distribution isn’t normal, the averages can be wildly different. In this case, nefarious people can pick the number that suits them best and simply label it the average.

Technique #2: Giving Precise Figures to Appear More Reputable

Another number-fudging technique is to include a decimal to make a figure look more precise and therefore reputable. (For example, reading that most people sleep 7.84 hours a night sounds a lot more impressive than “about eight hours.”)

Liars can get decimals by doing calculations (for example, calculating the mean) on inexact figures that weren't measured to the decimal point.

(Shortform example: If you ask 100 people how much they spent on groceries in the last month, they probably won’t remember exactly. Even if they give you round, approximate numbers, if you calculate the mean, you’ll likely end up with a decimal. For instance, (20+30+60)/3=36.66666... This number is meaninglessly more precise than the measures you started with, but it looks good.)

Technique #3: Using Percentages to Hide Numbers and Calculations

Here are some additional ways liars manipulate percentages and their associated terms for their gain:

(Shortform example #1: If a stock was worth $1 yesterday and $2 today, that’s a 100% increase, which looks impressive. However, the actual difference is only $1, which is less impressive.)
(Shortform example #2: If one person uses cold medicine and is cured, the liar can cite the medicine’s success rate as 100%.)

For example, The New York Times once reported that after taking a 20% pay cut last year, union workers got a 5% raise the next year, which gave them back one-fourth of their cut wage. This claim of it being one-fourth of their cut wage refers to 5% being one-fourth of 20%. However, the workers didn’t actually get 5% of their original wage back, they got 5% of their new, lower wage back, which is a smaller number. The 20% cut and the 5% increase were calculated off different bases, so weren’t directly comparable.

Liars can also combine percentages and averages while manipulating bases to mask the real data even more. For example, if milk has gone down from $2 a pint to $1, but bread has gone up from $1 to $2, liars can massage percentage math and choose different bases to prove the cost of living has gone up or down, depending on their agenda. To show costs went up, they can decide that last year’s prices were the base (100%). Milk’s price has halved (50%) and bread’s price has doubled (200%). The average of 50% and 200% is 125%, so prices have increased by 25% since last year.

To show costs went down, they can decide that this year is the base year (100%). With this base, milk used to cost 200% more and bread cost 50% less—you get the same average of 125%, but since the base is different, it shows a decrease of 25% since last year.

3. Adding up percentages. Percentages aren’t numbers—you can't meaningfully add or subtract them.

For example, imagine you buy 20 vegetables at the grocery store and all of them cost you 5% more than they did last year. If you add together all of those 5% increases, you get a 100% increase (20*5%=100%). This could be reported as “the cost of living has gone up by 100%.” But in reality, it hasn’t—it’s gone up by 5%, and all products were affected.

Technique #4: Using the Most Favorable Form

The fourth technique is to report numbers in whatever form most exaggerates or minimizes them; whichever will further a liar’s agenda. For example, return on sales, return on investment, and increase or decrease in profits are all ways of reporting how much money a company made. Most people won’t realize that each type of measure tells only part of the story. For example, if you buy a stock every morning for $99 and sell it in the afternoon for $100, you’re making only 1% on total sales, which doesn’t sound like a great return. However, over 30 days, you’re making 30% on total money invested—a much better-sounding prospect.

Example #1: If a liar thinks it will look bad to report a high, raw profit value (perhaps because then employees will demand raises), she might report the return on sales instead if it’s lower.
(Shortform example #2: If 60 out of 90 people survive an operation, a liar who wants to discourage people from having the operation might choose to report this as “one-third of people who undergo the operation die,” rather than the equally accurate but survival-focused “two-thirds of people live.”)

Technique #5: Omitting Statistical Qualifiers

1. Probable error. Probable error is a measure of how reliable a figure is, expressed as a range that the true result will fall between. (It’s impossible to find the single number that represents the true result because measuring systems aren’t perfectly accurate.) If you’re presented with a single figure, and aren’t given any indication of how reliable it is or what the probable error is, it may not be accurate at all.

For example, if an IQ test has a probable error of 3 and you score 98, this means that your IQ is somewhere between 95-101 (98-3=95, and 98+3=101). The real number is equally likely to be any number in that range. So, simply telling someone that your IQ is 98 isn’t accurate.

For example, the editor of Reader’s Digest solicited a study of cigarette smoke ingredients, and a lab produced a list of what ingredients made up the smoke from different cigarettes. All of the cigarettes were poisonous, but one, Old Gold, had slightly smaller quantities of poisons than the others. Technically, it was true that smoke from Old Gold cigarettes had fewer poisons (and Old Gold used this data, minus raw figures, to advertise), but the difference was negligible—smoking any cigarette was equally as unhealthy.

Exercise: Look for Fudged Numbers

There are five techniques liars use to fudge the numbers.

Imagine you read that the average income of an Ivy League graduate is $70,562. What lying techniques were possibly used in generating this stat? How do you know?
Imagine you read that a company’s return-on-investment has increased since last year by 1.34%. What lying techniques were possibly used in generating this stat? How do you know?

Chapter 3: Fudging the Point

In the previous chapter, you learned how liars massage math to make their results look more favorable. If liars can’t find a calculation that gives them figures they like, another technique they use is to focus on other figures that do seem to support what they have to say.

There are two techniques liars use to do this:

If liars can’t prove something, sometimes, they’ll prove something else that sounds like it's the same as what they were trying to prove.

For example, if a cold medicine company can’t prove that their drug cures colds, but they can prove that it kills germs in a lab, they might advertise that their medicine “kills 15,000 germs.” Killing germs isn’t the same as curing colds (colds probably aren’t even caused by germs), but they’re close enough that people might think the medicine actually works.

Note that in some cases, the semi-related figure can actually give a more accurate picture of the situation than the direct figure.

For example, the number of deaths a disease has caused is often a better indication of its incidence than the number of cases of it, because the record-keeping around fatalities is more robust.

Technique #2: Attributing Correlation to Causation

The next technique involves pushing the idea that if there’s a relationship between two factors, one of them caused the other, and whichever factor is most favorable to a liar’s argument is the cause.

For example, one study found that smokers got lower grades at college. A non-smoking activist with an agenda might report this as “If you stop smoking, your grades will improve.”

This is misleading because:

1. It’s often impossible to know which factor is the cause and which is the effect.

For example, people struggling with the stress of bad grades could be driven to smoking for relief: In other words, bad grades could be the cause of smoking, not the effect of it.

Sometimes, the two factors are so interrelated they both act as both cause and effect.

For example, stock ownership and income are probably both causes and effects at the same time. The higher your income, the more stocks you can afford, and since stocks make you money, the more stocks you have, the higher your income will be.

2. Both factors may be effects of some other cause. While the relationship between the factors is real, the cause-and-effect is uncertain.

For example, maybe the same people who smoke are the same people who have low grades because they like socializing more than studying.

3. The relationship between the two may be only due to chance.4. Even if there is a real cause-and-effect relationship, that doesn’t mean it applies to everyone. Correlations are tendencies.

For example, while it’s fairly conclusive that people who get a post-secondary education have higher incomes than those who don’t, that doesn’t mean that you will make more money if you go to college than if you don’t. (It’s also unknown if the people who make more money and also went to college might still have higher salaries even if they hadn’t gone to college—college attracts bright, rich people who already had a better chance at making more money.)

5. Correlations can be caused by humans and trends, rather than the factor you think they’re caused by.

For example, older women tend to walk with their toes farther apart than younger women. This is because posture trends changed over the years, not because women’s posture necessarily changes as they age (which is what some people may assume).

An advanced version of misleadingly attributing correlation to causation is to presume that the correlation extends beyond the data. For example, a study might find more rain results in better crops, and someone might assume that this correlation holds in all circumstances: in other words, that more and more rain always results in better crops. However, that relationship doesn’t hold forever—if the rain is so heavy it causes floods, the crops will suffer.

Chapter 4: Fudging the Graphics

In the previous two chapters, you learned seven techniques liars use to present numbers in the most favorable light. Now, we’ll look at another way they misleadingly report numbers—in images.

Here are some ways that liars lie in graphics. They:

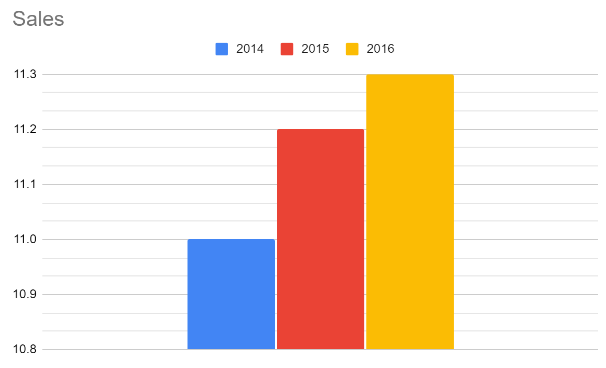
1. Truncate the graphs. To make changes look larger than they are, liars remove the empty space on a graph so that the part the data occupies is the only part shown. This will make the slope of a line look steeper, or the difference between bars look greater.

For example, from this graph, it’s clear that profit is steadily growing:

On this truncated graph, however, it appears that profit is rapidly growing, because the empty space is gone:

2. Add more divisions to the y-axis. Like truncation, this will visibly amplify the differences between measures.

For example, from this graph, it’s obvious that there’s little difference in profit from year-to-year:

In this graph, which uses the same data as the first graph but has more divisions and has been truncated, profit looks significantly different from year to year:

3. Leave the graph labels and numbers out. To be meaningful, diagrams and graphs need labels and numbers, otherwise, it’s impossible to know what they show.

For example, one advertising agency presented a graph that showed a steadily rising line. The y-axis showed time in years, but the x-axis had no label. Presumably, it was profit, but without numbers, it was impossible to know if profits were jumping by millions or cents.

4. In bar graphs, use illustrations instead of bars. In a bar chart, the height of the bar is what indicates the measurement. When you replace a bar with an illustration—say, a bag of money—when you increase the height of the moneybag, all the other dimensions scale proportionally. Increasing the width and depth (if 3-D) of the image makes the differences between the two images look much larger.

(Shortform example: In the illustration below, the skulls represent the death rate from a certain illness. Before a liar’s medication was adopted, the death rate was 60 out of 1 million, represented by a skull at height 60. After adoption, the death rate halved to 30, represented by a skull at height 30. However, visually, the rate appears to have dropped by far more than half because the image appears to have decreased by more than half: The whole image was scaled down proportionally, rather than just the height being halved.

This trick can also give the false impression, depending on the illustration, that whatever’s represented in the image is now larger than it used to be.

For example, if a graph compares the size of the cow population between two years, but uses two images of cows, one smaller and one bigger, people might think the size of cows has increased instead.

5. In before-and-after photos, change multiple things about the subject after the before picture has been taken to make the change look more significant than it really is.

For example, a photo of a woman before she started using a hair rinse might be taken with poor lighting and printed in black and white. In the after photo, she might be well-lit and smiling, and the photo might be printed large in full color. The after photo looks better not because the hair rinse made her hair look better, but because the photography was better.

6. In maps, use the many variables to create visual illusions. Since maps include many features (legends, border, different-sized regions, and so on), they’re excellent tools for misdirection.

For example, the First National Bank of Boston produced a map called “The Darkening Shadow” that showed how much of the national income is spent by the federal government. The spending was represented by shading in enough states that federal spending was equal to the total income of those states.

Of course, states have different areas and populations. The bank chose to shade the states with small populations (and therefore low total incomes) and large areas. As a result, their map shows over half of the western United States shaded, which makes federal spending look huge.

It would have been just as accurate to shade the small, highly populated states such as the ones on the eastern seaboard. Choosing this method, only a small portion of the map would be shaded, and the spending looks small—but this wouldn’t have suited First National’s agenda, so they didn’t do it.

Exercise: Assess a Graph

There are many techniques liars use to make graphs misleading.

Which of the liars’ techniques do you spot in the line graph below?
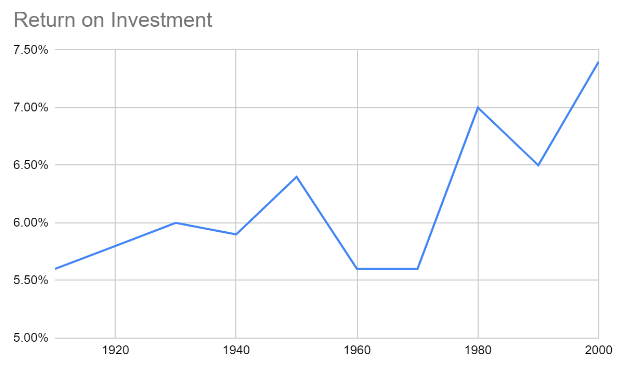
Which of the liars’ techniques do you spot in the bar graph below?

Chapter 5: Assessing the Legitimacy of Statistics

In the previous three chapters, you learned some of the strategies liars use to mislead people with statistics. Now, you’ll learn about a five-question checklist you can go through every time you encounter a statistic to assess its legitimacy. The goal is to find balance—you don’t want to swallow statistics without thinking about them (it’s often worse to know something wrong than to be ignorant), but you also don’t want to be so suspicious that you ignore all statistics and miss out on important information.

Here are the evaluation questions:

Question #1: What Is the Source of the Figure?

The first thing to do when confronted with a statistic is to figure out where it’s coming from. The source may not be obvious, because liars often borrow the numbers of reputable organizations, such as universities or labs, but come to their own conclusions. Then, they try to make it look like their conclusion is the reputable organization's conclusion. Always be suspicious of the phrase “the survey/study shows”; who says that the survey or study shows this?

For example, in an article about how women who attend college have a higher likelihood of becoming old maids, the writer cited data from Cornell about how many of its women students were married. Cornell did publish numbers about how many of its students were married, but the school didn’t draw any conclusions. The conclusion in the article—women who go to college are more likely to stay unmarried—came from the article’s writer, but since the data was from Cornell, it almost appeared as if the conclusion had come from Cornell.

Once you’ve determined the source, look for these two types of biases:

Conscious. If you think the statistic is coming from a liar with an agenda, look for the techniques covered in the chapters above.
Unconscious. If the bias is unconscious, there won’t be obvious clues that the figures are inaccurate (for instance, the vague use of the word “average,” without explaining which average they mean). If there are no signs of obvious lying, consider whether the source’s agenda is furthered by the figures it gives and if this might have blinded them to certain ideas or further explorations of the data.

Question #2: What Was the Data Collection Method?

The second question addresses the data collection method. Any data that’s based on what respondents say, or how motivated they are to respond to something in a certain way, can skew the truth because people aren't always truthful. When confronted with a statistic that was calculated based on people’s responses, ask yourself if there’s any reason the respondents might have been motivated to lie.

For example, one census in China, for military and tax purposes, found the population of one region to be 28 million. The next census, for famine relief purposes, found the population of the same region to be 105 million. The population hadn’t changed much over the five years in between censuses—people were just a lot keener to be counted when it meant famine relief than when it meant getting taxed.

Question #3: Is Any Relevant Information Omitted?

In the third question, you’ll consider the context of the statistic. If a figure is cited on its own, ask yourself if any of the following accompanying information exists, and if leaving it out would further anyone’s interests:

1. Statistical qualifiers. See Chapter 2 for a discussion of what numbers need to accompany stats (such as degree of significance) to make them meaningful.

2. Other relevant figures. Consider what additional context statisticians would need to take into account to come up with the most accurate figure possible.

For example, an environmentalist who wants the government to regulate pollution might cite a high death rate during pollution-related foggy weather in London and attribute the deaths to the fog. However, this doesn’t represent how the world works—people die for plenty of reasons that don’t have anything to do with the weather, and the high death rate could have been caused by something else. A more accurate statistic would be to cite the death rate accompanied by cause of death: This would show how many people truly died due to fog.

3. Cause. If an explanation for the figure isn’t included, ask yourself what it might be. (If a liar leaves out the real cause, they can imply an effect was prompted by a more desirable cause.)

For example, one retail company wanted to show that business was improving because this year’s April sales were better than last year’s. A quick check of the calendar shows that Easter had fallen in March the year before and in April that year. Holiday sales were more likely responsible for the boost than an overall improvement in business.

Question #4: Is the Language Surrounding the Figures Misleading?

Statistics are often reported in articles, surrounded by words (as opposed to in a table or chart). To answer this fourth question, study the words surrounding the figure and consider their definitions (to twist their results to suit their argument, liars may not use the most common definition of an everyday word, as you learned with “average”).

(Shortform example #1: Anything can be the “first” or “biggest” or “best” of its kind, depending on how people define these words. For instance, the “biggest” waterfall in Canada is Niagara Falls (if “big” means the largest volume of water falling) or Della Falls (if “big” means highest).)
Example #2: Accountants proposed using “retained earnings” or “appreciation of fixed assets” instead of the word “surplus” on corporate balance sheets. Most people know what surplus means, but not what the other words mean, so using these words in the balance sheets could hide how well companies were doing.
Example #3: In a statistical context, “normal” doesn’t mean “ideal” or “good;” it means “usual.” But since most people do associate “normal” with “good,” seeing the word paired with a statistic can leave them with inaccurate (and emotionally worrying) conclusions. For example, if you see a stat that says most children “normally” start talking at a certain age and your child doesn’t talk by that age, you might worry that she’s abnormal or behind, when this isn’t necessarily the case.

Question #5: Does that Figure Make Sense?

To answer this last question, don’t blindly trust numbers—consider if what they reveal actually makes sense.

There are four ways to assess a statistic against common sense:

1. Simply ask yourself if it seems right.

For example, according to the Rudolf Flesch readability formula, Plato’s Republic was significantly easier to read than “The Legend of Sleepy Hollow.” As Republic is a complicated, ethical dialogue written in 375 BC and “Sleepy Hollow” is a short story, it doesn’t seem right that the short story is more challenging to read.

2. Compare the figure to commonly known and reputable facts.

For example, one urologist calculated that there are eight million cases of prostate cancer in the US. At the time, the male population of the US was less than eight million, which meant the figure couldn’t be accurate.

3. Consider the figure’s precision. If the figure represents something abstract or difficult to measure (such as happiness), then it’s unlikely someone would have actually been able to measure it with a decimal point’s worth of precision.

4. Remember that extrapolation has limits. If a figure is based on extrapolation, be mindful that extrapolations are nothing more than educated guesses. Often, reality turns out to be much different from what the extrapolation predicted because things never continue to grow as you expect.

For example, based on population data from 1790 to 1860, Abraham Lincoln predicted that the country’s population would be over 150 million by 1930, which was very incorrect.

Exercise: Assess a Statistic

There are five questions to ask when you encounter a statistic to assess its legitimacy.

Consider this statistic published by a company selling blue wallpaper: “According to a survey of parents conducted by our company, an average of 97.68% of infants cry when in a room with green-colored wallpaper. Therefore, most infants hate living in homes with green wallpaper.” What is the original source of this stat? How might this affect its reliability?
How was the data that produced the stat collected? (For example, did interviewers poll people, was an online survey advertised on social media, and so on?) Can you think of any reason people who participated might have given untrue answers?
What missing information may be relevant to interpreting the statistic?
Could any of the words surrounding the statistic have more complicated meanings than what’s in the dictionary? What could they also mean?
Does the figure seem right? (For example, does it contradict common sense or have any obvious fact-checking errors?) Why or why not?

1-Page Summary

Technique #1: Misleading With Bad Sampling

Techniques #2-6: Fudging the Numbers (or the Point)

Technique #2: Citing Misleading “Averages”

Technique #3: Giving Precise Figures to Appear More Reputable

Technique #4: Using Percentages to Hide Numbers and Calculations

Technique #5: Omitting Statistical Qualifiers

Technique #6: Citing Semi-Related Figures

Technique #7: Attributing Correlation to Causation

Techniques #8-10: Manipulating Images

Technique #8: Truncating Graphs or Add More Divisions to the Y-Axis

Technique #9: Failing to Include Labels and Numbers on Graphs

Technique #10: In Bar Graphs, Using Illustrations Instead of Bars

Assessing the Legitimacy of Statistics

Chapter 1: Misleading With Bad Sampling

Good Sampling

Bad Sampling

Chapter 2: Fudging the Numbers

Technique #1: Citing Misleading “Averages”

Technique #2: Giving Precise Figures to Appear More Reputable

Technique #3: Using Percentages to Hide Numbers and Calculations

Technique #4: Using the Most Favorable Form

Technique #5: Omitting Statistical Qualifiers

Exercise: Look for Fudged Numbers

Chapter 3: Fudging the Point

Technique #1: Citing Semi-Related Figures

Technique #2: Attributing Correlation to Causation

Chapter 4: Fudging the Graphics

Exercise: Assess a Graph

Chapter 5: Assessing the Legitimacy of Statistics

Question #1: What Is the Source of the Figure?

Question #2: What Was the Data Collection Method?

Question #3: Is Any Relevant Information Omitted?

Question #4: Is the Language Surrounding the Figures Misleading?

Question #5: Does that Figure Make Sense?

Exercise: Assess a Statistic