TTTTTT

HTHTTH

However, sequence 3 “looks” far more random. Sequence 1 and 2 are more likely to trigger a desire for alternative explanations. (Shortform note: the illusion also occurs because there is only one such sequence of TTTTTT, but hundreds of the type like the third that we don’t strongly distinguish between.)

Corollary: we look for patterns where none exist.

Other examples:

• In World War II, London was bombed evenly throughout except for a few conspicuous gaps. Some suspected German spies were in those areas and thus those areas were deliberately saved. In reality, the distribution of hits were typical of a random process.
• There is no such thing as a hot hand in basketball - statistical analyses show that these streaks of baskets are entirely random.

Evolutionarily, the tendency to attribute patterns to randomness might have arisen out of a margin of safety for hazardous situations. That is, if a pack of lions suddenly seems to double, you don’t try to think about whether this is just a random statistical fluctuation. You just assume there’s a cause and impending danger, and you leave.

Causal Situations

Individual cases are often overweighted relative to statistics. In other words, even when we get accurate statistics about a situation, we still tend to focus on what individual cases tell us.

This was shown to great effect when psychology students were taught about troubling experiments like the Milgram shocking experiment, where 26 of 40 ordinary participants delivered the highest voltage shock.

Students were then shown videos of two normal-seeming people. These people didn’t seem the type to voluntarily shock a stranger. The students were asked: how likely were these individuals to have delivered the highest voltage shock?

The students guessed a chance far below 26/40, the statistical rate they had just been given.

This is odd. The students hadn’t learned anything at all! They had exempted themselves from the conclusions of experiments. “Surely the people who administered the shocks were depraved in some way - I would have behaved better, and normal people like these two folks would as well.” They ignored the statistics in favor of the individual cases given to them.

The antidote to this was to reverse the order - students were told about the experimental setup, shown the videos of the two people, and only then told the outcome of how 26 out of 40 ordinary participants had delivered the maximum shock. Their estimate of the failure rate of the two individuals became much more accurate.

Reversion to the Mean

Over repeated sampling periods, outliers tend to revert to the mean. High performers show disappointing results when they fail to continue delivering; strugglers show sudden improvement.

In reality, this is just statistical fluctuation. However, as the theme of this section suggests, we tend to see patterns where there are none. We come up with cute causal explanations for why the high performers faltered, and why the strugglers improved.

Here are examples of reversion to the mean:

• A military commander has two units return, one with 20% casualties and another with 50% casualties. He praises the first and berates the second. The next time, the two units return with the opposite results. From this experience, he “learns” that praise weakens performance and berating increases performance.
• In the Small Numbers example above, if the Gates Foundation had measured the schools again in subsequent years, they’d find the top-performing small schools would have lost their top rankings.
• Many health problems tend to resolve on their own, given our bodies’ natural healing properties. However, patients attribute the healing to whatever action they took meanwhile - seeing a doctor, doing a superstitious act, taking medicine - while ignoring that they likely would have returned to full health without any action.
• Athletes on the cover of Sports Illustrated seem to do much worse after being featured. This is explained as the athlete buckling under the pressure of being put under the spotlight. In reality, this could simply be because the athlete had had an outlier year (which got them the attention to get on the cover) and has now reverted to the mean.
• In dating, there is an idea that intelligent women tend to marry men who are less intelligent than they are. The reasons given are that smart men are threatened by intelligence, or that smart women want to be dominant. The statistical explanation is that intelligent women are a minority of women (by definition of the bell curve), and so when an intelligent woman marries a man, the man is simply statistically more likely to be less intelligent than the woman.
• The majority of mutual funds do not deliver returns better than the market, after deducting fees. However, individually, they may do well one year or another and thus have the appearance of shrewd financial insight.
• Publications like Fortune often release a list of “Most Admired Companies.” Over time, they find that the firms with the worst ratings earn much higher stock returns than the most admired firms. The causal explanation given is that the top firms rest on their laurels, while the worst companies get inspiration from being ranked poorly. In reality, both types of firms are just reverting to the mean.

Reversion to the mean occurs when the correlation between two measures is imperfect, and so one data point cannot predict the next data point reliably. The “phenomena” above can be restated in these terms: “the correlation between year 1 and year 2 of an athlete’s career is imperfect”; “the correlation of performance of a mutual fund between year 1 and year 2 is imperfect.”

In other words, when we ignore reversion to the mean, we overestimate the correlation between the two measures. When we see an athlete with an outlier performance in one year, we expect that to continue. When it doesn’t, we come up with causal explanations rather than realizing we simply overestimated the correlation.

These causal explanations can give rise to superstitions and misleading rules (“I swear by this treatment for stomach pain.”)

Antidote to this bias: when looking at high and low performers, question what fundamental factors are actually correlated with performance. Then, based on these factors, predict which performers will continue and which will revert to the mean.

Part 2-2: Anchors

Anchoring describes the bias where you depend too heavily on an initial piece of information when making decisions.

In quantitative terms, when you are exposed to a number, then asked to estimate an unknown quantity, the initial number affects your estimate of the unknown quantity. Surprisingly, this happens even when the number has no meaningful relevance to the quantity to be estimated.

Examples of anchoring:

• Students are split into two groups. One group is asked if Gandhi died before or after age 144. The other group is asked if Gandhi died before or after age 32. Both groups are then asked to estimate what age Gandhi actually died at. The first group, who were asked about age 144, estimated a higher age of death than students who were asked about age 32, with a difference in average guesses of over 15 years.
• Students were shown a wheel of fortune game that had numbers on it. The game was rigged to show only the numbers 10 or 65. The students were then asked to estimate the % of African nations in the UN. The average estimates came to 25% and 45%, based on whether they were shown 10 or 65, respectively.
• A nonprofit requested different amounts of donations in its requests. When it requested $400, the average donation was $143; when requesting $5, the average donation was $20.
• In online auctions, the Buy Now prices serve as anchors for the final price.
• Arbitrary rationing, like supermarkets with “limit 12 per person,” makes people buy more cans, compared to when there’s no limit. (Shortform note: this might also be confounded as a signal of demand, indicating quality or scarcity.)

Note how in several examples above, the number given is not all that relevant to the question at hand. The wheel of fortune number has nothing to do with African countries in the UN; the requested donation size should have little effect on how much you personally want to donate. But it still has an effect.

Sometimes, the anchor works because you infer the number is given for a reason, and it’s a reasonable place to adjust from. But again even meaningless numbers, even dice rolls, can anchor you.

The anchoring index measures how effective the anchor is. The index is defined as: (the difference between the average guesses when exposed to two different anchors) / (the difference between the two anchors). Studies show this index can be over 50%! (A measure of 100% would mean the person in question is not only influenced by the anchor but uses the actual anchor number as their estimate; conversely, a measure of 0% would indicate the person has ignored the anchor entirely.)

• For example, one study asked Group A two questions: 1) Is the tallest redwood taller or shorter than 1,200 feet? and 2) What do you think the height of the tallest redwood is? They asked Group B the same two questions, except the anchor in the first question was 180 feet rather than 1,200 feet.
• Did the anchors in the first question affect the estimates given in answer to the second question? Yes. The Group A mean was 844 feet and the Group B mean was 282 feet. This produced an anchoring index of 55%.

Insidiously, people take pride in their supposed immunity to anchored numbers. But you really don’t have full command of your cognition.

• When you’re buying a house, real estate agents claim to be immune to listing prices when negotiating prices for you, when the opposite is true. The listing price strongly anchors agents to the bid that they make.

(Shortform note: the idea of anchoring can be taken beyond numbers into ideas. If someone tells you an extremely outrageous idea, then later gives you a second idea that is less extreme, the second idea sounds less controversial than if he had presented it to you first. That’s because you’ve anchored to the first extreme idea.)

Why Anchoring Works

How does anchoring work in the brain? There are two mechanisms, based on the two systems of thinking.

System 2: You start with the exposed number as an initial guess, then adjust in one direction until you’re not confident you should adjust further. At this point you’ve reached the edge of your confidence interval, not the middle of it.

• Say you were given a piece of paper and asked to draw from the bottom up until you reached 2.5 inches. Then you were asked to draw, on a separate sheet of paper, from the top down until 2.5 inches were left. The first line would likely be shorter than the space below the second line. This is because you’re not really sure what 2.5 inches looks like. If you think of uncertainty as a range, you stop drawing at the bottom edge of your uncertainty, when you first lose confidence. You stop when you reach the edge of the confidence range, not the middle of it.
• You drive much faster on city streets coming off the highway than you would otherwise because your anchor is higher than when you start from, say, a speed of zero in your driveway. You adjust relative to your anchor.
• If asked about the boiling temperature of water at the top of Mount Everest, you know that the boiling point of water at sea level is 100° Celsius, but you know that can’t be the answer to the question, since the top of Mount Everest is obviously not at sea level. To estimate the answer, you use 100° Celsius as your anchor and adjust downwards.
• Evidence that System 2 is involved: People adjust less from the anchor when their mental resources are depleted and, therefore, System 2 isn’t working well.

System 1: The anchor invokes associations that influence your thinking. System 1 tries to construct a world in which the anchor is the true number.

• Thinking of Gandhi as age 144 primes associations of old age. This causes a higher estimate.
• Evidence that System 1 is involved: Asking participants whether the average temperature was higher or lower than 68°F made it easier to recognize summer words (like “beach”) in a list. Similarly, asking about 41°F made it easier to identify winter words (like “ski”).

Overcoming Anchors

In negotiations, when someone offers an outrageous anchor, don’t engage with an equally outrageous counteroffer. Instead, threaten to end the negotiation if that number is still on the table.

(Shortform suggestions:

• If you’re given one extreme number to adjust from, repeat your reasoning with an extreme value from the other direction. Adjust from there, then average your final two results.
• When estimating, first adjust from the anchor to where you feel like you should stop. Then deliberately go much further to the point that you want to dial it back. Average the two points.
• Move your estimate from the anchor to the minimal or maximal amount it could be.)

Part 2-3: Availability Bias

When trying to answer the question “what do I think about X?,” you actually tend to think about the easier but misleading questions, “what do I remember about X, and how easily do I remember it?” The more easily you remember something, the more significant you perceive what you’re remembering to be. In contrast, things that are hard to remember are lowered in significance.

More quantitatively, when trying to estimate the size of a category or the frequency of an event, you instead use the heuristic: how easily do the instances come to mind? Whatever comes to your mind more easily is weighted as more important or true. This is the availability bias.

This means a few things:

• Items that are easier to recall take on greater weight than they should.
• When estimating the size of a category, like “dangerous animals,” if it’s easy to retrieve items for a category, you’ll judge the category to be large.
• When estimating the frequency of an event, if it’s easy to think of examples, you’ll perceive the event to be more frequent.

In practice, this manifests in a number of ways:

• Events that trigger stronger emotions (like terrorist attacks) are more readily available than events that don’t (like diabetes), causing you to overestimate the importance of the more provocative events.
• More recent events are more available than past events, and are therefore judged to be more important.
• More vivid, visual examples are more available than mere words. For instance, it’s easier to remember the details of a painting than it is to remember the details of a passage of text. Consequently, we often value visual information over verbal.
• Personal experiences are more available than statistics or data.
  • Famously, spouses were asked for their % contribution to household tasks. When you add both spouses’ answers, the total tends to be more than 100% - for instance, each spouse believes they contribute 70% of household tasks. Because of availability bias, one spouse primarily sees the work they had done and not their spouse’s contribution, and so each spouse believes they contributed unequally more.
• Items that are covered more in popular media take on a greater perceived importance than those that aren’t, even if the topics that aren’t covered have more practical importance.

As we’ll discuss later in the book, availability bias also tends to influence us to weigh small risks as too large. Parents who are anxiously waiting for their teenage child to come home at night are obsessing over the fears that are readily available to their minds, rather than the realistic, low chance that the child is actually in danger.

Availability Bias and the Media

Within the media, availability bias can cause a vicious cycle where something minor gets blown out of proportion:

• A minor curious event is reported. A group of people overreact to the news.
• News about the overreaction triggers more attention and coverage of the event. Since media companies make money from reporting worrying news, they hop on the bandwagon and make it an item of constant news coverage.
• This continues snowballing as increasingly more people see this as a crisis.
• Naysayers who say the event is not a big deal are rejected as participating in a coverup.
• Eventually, all of this can affect real policy, where scarce resources are used to solve an overreaction rather than a quantitatively more important problem.

Kahneman cites the example of New York’s Love Canal in the 1970s, where buried toxic waste polluted a water well. Residents were outraged, and the media seized on the story, claiming it was a disaster. Eventually legislation was passed that mandated the expensive cleanup of toxic sites. Kahneman argues that the pollution has not been shown to have any actual health effects, and the money could have been spent on far more worthwhile causes to save more lives.

He also points to terrorism as today’s example of an issue that is reported widely by the media. As a result, terrorism is more available in our minds than the actual danger it presents, where a very small fraction of the population dies from terrorist attacks.

Kahneman is sympathetic to the biases, however—he notes that even irrational fear is debilitating, and policymakers need to protect the public from fear, not just real dangers.

Running Out of Availability Makes You Less Confident

A series of experiments asked people to list a number of instances of a situation (such as 6 examples of when they were assertive). Then they were asked to answer a question (such as “evaluate how assertive you are”).

Question: what has a greater effect on a person’s perception of how assertive they are—the number of examples they can come up with, or the ease of recall? In other words, does someone who comes up with 10 examples of when they are assertive feel more confident than someone who comes up with 3?

You might think more examples would strengthen conviction, but being forced to think of more examples actually lowers your confidence. When people are asked to name 6 examples of their assertiveness, they feel more assertive than those asked to name 12 examples. The difficulty of scraping up the last few examples dampens one’s confidence.

Similarly, people are less confident in a belief when they’re asked to produce more arguments to support it. The act of scraping the bottom of the barrel for ideas gives you the feeling that your ideas are less available, which then weakens your belief.

There are some exceptions to this effect:

• When people are given a cover story for their difficulty in recall, this effect dissipates.
  • For example, in a variant of the assertiveness experiment above, subjects were told that listening to a particular piece of music would impair their recall ability. People who were asked to name 12 examples of assertiveness rated themselves equally assertive as those asked to name 6. Having a reason for being worse at recall prevented them from being demoralized by it.
  • Profoundly, this means System 2 can influence how surprised System 1 feels. This is analogous to being told before you meet someone, “the man you’re about to meet has 7 fingers—don’t be surprised.”
• This effect reverses when someone has had personal experience with the situation.
  • When asked about what behaviors would prevent disease, people with a family history of heart disease felt safer when they retrieved more instances. In this case, they weren’t bothered by how difficult the last items were to recall - the more they could think of, the better they felt.

Antidotes to Availability Bias

The conclusion is that System 1 uses ease of recall as a heuristic, while System 2 focuses on the content of what is being recalled, rather than just the ease. Therefore, you’re more susceptible to availability bias when System 2 is being taxed.

Experiments also show that you’re more susceptible to availability:

• When you’re in a good mood
• When you’re a novice in the field rather than an expert
• When you’re made to feel powerful and successful

(Shortform note: To counteract availability bias, think deliberately about what you are recalling and assign weights to their significance. This will avoid overestimating things that are just easy to remember.

For example, when thinking of reasons for and against quitting your job, write down all the reasons, then score each reason by significance rather than biasing toward the reasons that you remember most easily.

When estimating the number of deaths by lightning strikes or diabetes, estimate it first from principle—how many people have diabetes, and how many have died from lightning strikes? What official numbers can you remember to ground your estimate? Don’t start from what you remember about each, whether it’s a news story about a lightning strike or a family member with diabetes.)

Part 2-4: Representativeness

Read the following description of a person.

Tom W. is meek and keeps to himself. He likes soft music and wears glasses. Which profession is Tom W. more likely to be? 1) Librarian. 2) Construction worker.

If you picked librarian without thinking too hard, you used the representativeness heuristic - you matched the description to the stereotype, while ignoring the base rates.

Ideally, you should have examined the base rate of both professions in the male population, then adjusted based on his description. Construction workers outnumber librarians by 10:1 in the US - there are likely more shy construction workers than all librarians!

More generally, the representativeness heuristic describes when we estimate the likelihood of an event by comparing it to an existing prototype in our minds - matching like to like. But just because something is plausible does not make it more probable.

The representativeness heuristic is strong in our minds and hard to overcome. In experiments, even when people receive data about base rates (like about the proportion of construction workers to librarians), people tend to ignore this information, trusting their stereotype matching more than actual statistics.

(Shortform note: even after reading this, you might think - but what about self-selection? Don’t meek people tend to seek library jobs and stay away from construction jobs? Isn’t it possible that all the shy librarians outnumber all the shy construction workers, even though there are 10 times more construction workers than librarians? This just goes to show how entrenched the representativeness heuristic is—you seek to justify your stereotype rather than looking at the raw data.)

Here’s another example:

Someone on the subway is reading the New York Times. Is the stranger more likely to have a PhD, or to not have a college degree?

Again, by pure number of people, there are far more people in the latter group than the former.

Why Do We Suffer from the Representativeness Heuristic?

Representativeness is used because System 1 desires coherence, and matching like to like forms a coherent story that is simply irresistible.

The representativeness heuristic works much of the time, so it’s hard to tell when it leads us astray. Say you’re shown an athlete who’s thin and tall, then asked which sport he plays. You’d likely guess basketball more than football, and you’d likely be correct.

(Shortform note: the representativeness heuristic causes problems when your System 1 forms a coherent story that is inaccurate. Common problems involve stereotypes that cause incorrect snap judgments:

• When hiring for a role, you might hire based on a stereotype of how that role should behave, rather than the work the person does. For example, if you expect engineers to be plain and soft-spoken, a candidate who’s fashionable and outgoing might strike you as suspicious.
• While in the Israeli army, Kahneman was tasked with evaluating which recruits would be best suited for officer positions. He confidently gave predictions based on what he observed, writing notes like “this person is a certain star,” only to later find out his predictions were only slightly better than chance.
• We tend to elect political leaders based on how they look and whether they fit our personal stereotype of what a leader should look like.)

Antidote to Representativeness Heuristic

System 1 desires a coherent story. Take away this convenient story, and you engage System 2. In the Tom W. question above, when students are asked to estimate the % of the population working in construction or libraries, the guesses are far more accurate. System 1 no longer has a stereotype to be led astray.

In general, the way to overcome the representativeness heuristic is to use Bayesian statistics. Start by predicting the base rates, using whatever factual data you have. Then consider how the new data should influence the base rates.

For example, in the New York Times example above, start by estimating the % of people who have a PhD and the % who have a college degree. Say you think that 2% of people have a PhD, and 50% have a college degree. Therefore, any random person would be 25 times more likely to have a college degree than a PhD. Then, when you receive the new information that the person is reading the New York Times, think about how that would influence movement from the base rates you estimated. You’ll likely end up with a more accurate estimate than if you didn’t estimate the base rate.

(Shortform note: to counter stereotypes, think about what factors matter, and how you’ll measure whether someone matches those factors. For example, when hiring for a job, think about what skills you need in the job and how you’ll measure whether a job candidate shows those skills. With these objective criteria, you’ll avoid relying on stereotypes.)

Conjunction Fallacy

Related to the representativeness heuristic is the conjunction fallacy. The best way to illustrate this is with an example.

Linda is 31 years old, single, outspoken, and very bright. She majored in philosophy. As a student, she was deeply concerned with issues of discrimination and social justice, and also participated in anti-nuclear demonstrations.

Which is more probable?

1. Linda is a bank teller.

2. Linda is a bank teller and is active in the feminist movement.

If you guessed 2, you fell for the conjunction fallacy. 1 is clearly a broader option than 2—there are many bank tellers who aren’t active in the feminist movement—so 1 should always be more likely. However, 2 explicitly mentioned a coherent story and thus seemed more representative of Linda, even though it’s more statistically unlikely.

(If you fell for this, don’t feel bad—over 85% of undergraduate students chose the second option.)

Here’s another example. Pick which event is more likely:

1. A massive flood in North America in which more than 1,000 people drown.

2. An earthquake in California that causes a flood in which more than 1,000 people drown.

The latter sounds more plausible because of the vividness of its detail—you can picture the cause of the flood. But it’s certainly less probable.

This is a problem when listening to forecasters—adding details to scenarios makes them more persuasive, but less likely to come true.

(Shortform note: if you’re interested, here’s a link with more examples.)

Antidotes to Conjunction Fallacy

Surprisingly, this fallacy is not invoked when a story doesn’t have coherence:

Which is more probable?

1. Mark has hair.

2. Mark has blond hair.

System 1 doesn’t have a chance to build an overall narrative here, so it becomes a pure statistical problem, and System 2 takes over. Many more people get the correct answer here.

Interestingly, there is a way to remove the bias by focusing people to name specific quantities, rather than just estimate percentages. Using the Linda example again, the questions would change to:

There are 100 people who fit the description above. How many of them are:

• Bank tellers? __ of 100

• Bank tellers and active in the feminist movement? __ of 100

When presented this way, many people realize the fallacy and change their answers to be statistically valid. Kahneman suggests this might be because this framing causes people to visualize 100 people in a room, and then they realize it’s clearly a mistake to have the group of feminist bank tellers be larger than the group of bank tellers.

More antidotes to conjunction fallacy:

• When hearing a complicated explanation that has too many convenient assumptions or vivid details (like an investment pitch for a business or an explanation for what caused a phenomenon), be aware that each additional assumption lowers the likelihood of it being true.
• When asked to estimate probability or percentages, think about a finite number, like 100 people.

Sets and Averages

The last example in the theme of representativeness is how the average value of a set of items can confuse us about its total value. Here’s an example:

Which is more valuable?

1. 24 dinner plates

2. 30 dinner plates, 5 of them broken

When viewed like this, the question is easy. The second option with 5 broken plates should be strictly more valuable because it has 25 intact dishes, whereas the first option only has 24.

But when viewed separately, people who view only option 1 are willing to pay more than people who view only option 2. The presence of broken dinner plates “pollutes” the set, and people average the whole set less.

As discussed earlier, System 1 is good at considering the average of items, but not so good at calculating the sum of items. Here, people use the heuristic—what is the average value of the plate in each set?—rather than considering the total value of all plates.

Part 2-5: Overcoming the Heuristics

As we’ve been discussing, the general solution to overcoming statistical heuristics is by estimating the base probability, then making adjustments based on new data. Let’s work through an example.

Julie is currently a senior in a state university. She read fluently when she was four years old. What is her grade point average (GPA)?

People often compute this using intensity matching and representativeness, like so:

• Reading fluently at 4 puts her at, say, the 90th percentile of all kids.
• The 90th percentile GPA is somewhere around a 3.9.
• Thus Julie likely has a 3.9 GPA.

Notice how misguided this line of thinking is! People are predicting someone’s academic performance 2 decades later based on how they behaved at 4. System 1 pieces together a coherent story about a smart kid becoming a smart adult.

The proper way to answer questions like these is as follows:

• Start by estimating the average GPA - this is the base data if you had no information about the student whatsoever. Say this is 3.0.
• Determine the GPA that matches your impression of the evidence. In this case, you might think someone who was fluent when she was 4 years old would have a GPA of 3.9.
• Estimate the correlation between your evidence and GPA. Do you think fluent reading at 4 years old is 100% correlated with academic success in college? Likely not—there are factors that affect reading age that aren’t relevant to college GPA, and vice versa. Is it 10% correlated? 50%?
• FInally, depending on the strength of your correlation, move from the average GPA from the first step to your estimated GPA in the second step. If you believe the correlation is just 10%, then you would move 10% from 3.0 to 3.9, ending up at around 3.1.

This methodical approach is generalizable to any similar prediction task. It avoids overly extreme results from intuition, instead using base rates and assessing the quality of information. It allows for regression toward the mean (eg replace “average GPA and student’s GPA” with “day 1 golf score and day 2 golf score”).

Are Smart Predictions Always Good?

Kahneman notes that absence of bias is not always what matters most. Relying too much on statistics would avoid the prediction of rare or extreme events on shaky information.

For example, venture capitalists make their money by correctly predicting the few companies that will make it big. They lose only 1x their money on a bad investment but make 1000x their money on a Google, so it’s important not to miss out on the next Google. However, using the type of quantitative analysis above might paralyze some investors, if they start with the baseline failure rate of startups (which is very high) and have to adjust upward from that anchor. For some people prone to paralysis, having distorted overoptimistic evidence might be better.

Similarly, sometimes the evidence is against you but your choice feels right, like when you know the high divorce rate as you’re about to get married. In these cases, you might be happier deluding yourself with extreme predictions—”our marriage is going to defy the odds.” Listening to our intuitions is more pleasant and less hard work than acting consciously against them. But at the least, be aware of what assumptions you are making and understand how much you know.

Part 3: Overconfidence | 1: Flaws In Our Understanding

Part 3 explores biases that lead to overconfidence. With all the heuristics and biases described above working against us, when we construct satisfying stories about the world, we vastly overestimate how much we understand about the past, present, and future.

The general principle of the biases has been this: we desire a coherent story of the world. This comforts us in a world that may be largely random. If it’s a good story, you believe it.

Insidiously, the fewer data points you receive, the more coherent the story you can form. You often don’t notice how little information you actually have and don’t wonder about what is missing. You focus on the data you have, and you don’t imagine all the events that failed to happen (the nonevents). You ignore your ignorance.

And even if you’re aware of the biases, you are nowhere near immune to them. Even if you’re told that these biases exist, you often exempt yourself for being smart enough to avoid them.

The ultimate test of an explanation is whether it can predict future events accurately. This is the guideline by which you should assess the merits of your beliefs.

Narrative Fallacy

We desire packaging up a messy world into a clean-cut story. It is unsatisfying to believe that outcomes are based largely on chance, partially because this makes the future unpredictable. But in a world of randomness, regular patterns are often illusions.

Here are a few examples of narrative fallacy:

• History is presented as an inevitable march of a sequence of events, rather than a chaotic mishmash of influences and people. If the past were so easily predictable in hindsight, then why is it so hard to predict the future?
• Management literature profiles the rise and fall of companies, attributing company growth to key decisions and leadership styles, even the childhood traits of founders. These stories ignore all the other things that didn’t happen that could have caused the company to fail (and that did happen to the many failed companies that aren’t profiled - survivorship bias). Ignoring this, the stories are presented as inevitabilities.
  • The book Built to Last profiled companies at the top of their field; these companies did not outperform the market after the book was published.
• Management literature also tries to find patterns to management systems that predict success. Often, the results are disappointing and not enduring.
  • The correlation between a firm’s success and the quality of its CEO might be as high as .30, which is lower than what most people might guess. Practically, this correlation of .30 suggests that the stronger CEO would lead the stronger firm in 60% of pairs, just 10% better than chance.
• We readily trust our judgments in situations that are poor representatives of real performance (like in job interviews).

Funnily, in some situations, an identical explanation can be applied to both possible outcomes. Some examples:

• During a day of stock market trading, an event might happen, like the Federal Reserve System lowering interest rates. If the stock market goes up, people say investors are emboldened by the move. If the stock market goes down, people say investors were expecting greater movement, or that the market had already priced it in. That the same explanation can be given, regardless of whether the market moves up or down, means that it’s likely a bad explanation with no predictive power.
• A CEO is known for his methodical, rigid style. If his company does well, they compliment him for sticking to his guns with clearly the right strategy. If the company falters, they blame his inflexibility to adapt to new situations.

Even knowing the narrative fallacy, you might still be tempted to write a narrative that makes sense—for example, successful companies become complacent, while underdogs try harder, so that’s why reversion to the mean happens. Kahneman says this is the wrong way to think about it—the gap between high performers and low performers must shrink, because part of the outcome was due to luck. It’s pure statistics.

There are obviously factors that correlate somewhat with outcomes. The founders of Google and Facebook are likely more skilled than the lower quartile of startups. Warren Buffett’s experience and knowledge is likely a good contributor to his investing success, and you’d be more successful if you replicated it. The key question is - how strong is the correlation?

Clearly a professional golfer can beat a novice perhaps 100% of the time. However, skill is the dominant factor here - the correlation is very high, so predictability is very high. In contrast, if you took the management principles espoused in business literature and tried to predict company outcomes, you might find they predict little. The correlation between management principles and company outcomes is likely low, which then means that a company’s success or failure is likely not due to their management practices.

Antidotes to Narrative Fallacy

Be wary of highly consistent patterns from comparing more successful and less successful examples. You don’t know lots of things—whether the samples were cherrypicked, whether the failed results were excluded from the dataset, and other experimental tricks.

Be wary of people who declare very high confidence around their explanation. This suggests they’ve constructed a coherent story, not necessarily that the story is true.

Hindsight Bias

Once we know the outcome, we connect the dots in the past that make the outcome seem inevitable and predictable.

Insidiously, you don’t remember how uncertain you were in the past—once the outcome is revealed, you believe your past self was much more certain than you actually were! It might even be difficult to believe you ever felt differently. In other words, “I knew it all along.” You rewrite the history of your mind.

• Imagine all the people who believe they foresaw the 2000 dotcom bubble bursting or the 2008 financial crisis happening.
• Professional forecasters (eg experts who show up on talk shows) perform no better than chance in predicting events. This might also be because they’re hired for their charisma and vocalness, not accuracy.

Hindsight bias is a problem because it inflates our confidence about predicting the future. If we are certain that our past selves were amazing predictors of the future, we believe our present selves to be no worse.

Outcome BIas

Related to hindsight bias, outcome bias is the tendency to evaluate the quality of a decision when the outcome is already known. People who succeeded are assumed to have made better decisions than people who failed.

This causes a problem where people are rewarded and punished based on outcome, not on their prior beliefs and their appropriate actions. People who made the right decision but failed are punished more than those who took irresponsible risks that happened to work out.

(Shortform note: to push the logic further, this causes problems in the future for continuing success. People who got lucky will be promoted but won’t be able to replicate their success. In contrast, the people who made good decisions won’t be promoted and in the position to succeed in the future.)

A few examples of outcome bias:

• An experiment used a legal case to ask subjects whether the city should have done a certain preventative action. When exposed to the evidence the city had at the time, 24% of people felt they should have taken the action. When exposed to the outcome the action was supposed to prevent, this rose to 56% of people!
• After September 11th, the US government was criticized for ignoring information about al-Qaeda in July 2001. But this ignores how little they could predict that September 11th would result from that piece of information.

The natural consequence of a reward system subject to outcome bias is bureaucracy - if your decisions will be scrutinized but the outcome is unpredictable, it’s better to follow rigid procedures and avoid risks. If you have proof that you followed directions, then even if your project ends up a failure, you won’t take the blame.

(Shortform note: antidotes to hindsight and outcome bias include:

• Keeping a journal of your current beliefs and what you estimate the outcomes to be. In the future, once the outcomes are known, reflect on your beliefs at the time to see how accurate you were.
• Rewarding people based on the decisions they make at the time with the information they had, before the outcomes come out. Don’t reward people who took outlandish risks but got lucky.)

We Mostly Don’t Accept These Biases

Even when presented with data of your poor predictions, you do not tend to adjust your confidence in your predictions. You forge on ahead, confident as always, discarding the news.

Kahneman argues the entire industry of the stock market is built on an illusion of skill. People know that on average, investors do not beat market returns (by definition, since the market is an average of all traders in the market, this must be the case). And plenty of studies show that retail investors trade poorly, against best practices—they sell rising stocks to lock in the gains, and they hang on to their losers out of hope, even though both are exact opposites of what they should do. In turn, large professional investors are happy to take advantage of these mistakes. But retail traders continue marching on, believing they have more skill than they really do.

Here are many reasons it’s so difficult to believe randomness is the primary factor in your outcomes, and that your skill is worse than you think:

• Pride and ego are at stake.
  • The more famous the forecaster, the more overconfident and flamboyant the predictions.
  • Experts resist admitting they’re wrong, instead giving excuses: they were wrong only in timing; they would have been right, but an unforeseeable event had intervened; or they were wrong, but for the right reasons.
• You take deliberate, skillful steps to guide the outcome. By producing a lot of motion, you think that you can’t be wrong.
  • Stock analysts pore over financial statements and build models. This requires lots of training and makes stock picking seem more rigorous. But this doesn’t answer the real, more difficult question - is the information already priced into the stock?
  • Managers focus on the strength of their strategy and how good their company seems, discounting what their competitors are doing and market changes (“competition neglect”).
  • Your experience shows many instances where your predictions came true —partially because those are most available to you, and you discount your mistakes.
• You focus on the causal role of skill and neglect the role of luck - the illusion of control.
• You don’t know what you don’t know. You aren’t aware of most of the factors that influence the final outcome, focusing on only the patterns that you do see.
• Large monetary incentives are at stake. You are being paid for your skill - if your skill turns out to be irrelevant, you’ll lose your job.
  • A survey of CFOs asked them to predict the “80% confidence interval” of stock market returns. When you ask someone to make an estimate, the 80% confidence interval is the range between a value the person is 90% sure is too high to be correct and a value the person is 90% sure is too low to be correct. Any result outside this range is considered a “surprise.” The CFOs’ guesses were far too narrow. An accurate 80% confidence interval would only be surprised 20% of the time; but the survey results showed surprises 67% of the time. The real 80% confidence interval was between -10% and +30% returns that year—but any CFO who says this would be criticized as lacking any knowledge.
  • It’s a sign of weakness to be unsure. It can have material marketing consequences to customers or investors, or to staff who want more certainty.
• Strong social proof in your community can maintain a belief in skill—if all these other smart people believe skill influences the outcome, then they can’t be wrong.
• Emergencies call for decisive action. In stressful situations, people desire certainty even more. Ambivalent decision making is criticized during these stressful times.

Part 3-2: Formulas Beat Intuitions

Humans have to make decisions from complicated datasets frequently. Doctors make diagnoses, social workers decide if foster parents are good, bank lenders measure business risk, and employers have to hire employees.

Unfortunately, humans are also surprisingly bad at making the right prediction. Universally in all studies, algorithms have beaten or matched humans in making accurate predictions. And even when algorithms match human performance, they still win because algorithms are so much cheaper.

Why are humans so bad? Simply put, humans overcomplicate things.

• They inappropriately weigh factors that are not predictive of performance (like whether they like the person in an interview).
• They try too hard to be clever, considering complex combinations of features when simply weighted features are sufficient.
• Their judgment varies moment to moment without them realizing it. System 1 is very susceptible to influences without the conscious mind realizing. The person’s environment, current mood, state of hunger, and recent exposure to information can all influence decisions. Algorithms don’t feel hunger.
  • As an example, radiologists who read the same X-ray twice give different answers 20% of the time.
• Even when given data from the formula, humans are bad! They feel falsely they can “override” the formula because they see something that’s not accounted for.

Simple algorithms are surprisingly good predictors. Even formulas that put equal weighting on its factors can be as accurate as multiple-regression formulas, since they avoid accidents of sampling. Here are a few examples of simple algorithms that predict surprisingly accurately:

• How do you predict marital stability? Take the frequency of sex and subtract the frequency of arguments.
• How do you predict whether newborns are unhealthy and need intervention? A while back, doctors used their (poor) judgment. Instead, in 1952 doctor Virginia Apgar invented the Apgar score, a simple algorithm that takes into account 5 factors, such as skin color and pulse rate. This is still in use today.
• How do you predict wine prices for a bottle of wine? Traditionally, wine enthusiasts tasted the bottle, then assigned a hypothetical price. Instead, an economist used only two variables—the summer temperature and rainfall of the vintage. This was more accurate than humans, but wine experts were aghast—“how can you price the wine without tasting it?!” The formula was in fact better because it did not factor in human taste.

There is still some stigma about life being pervaded by robotic algorithms, removing some of the romance of life.

• Professionals who use intuition to predict things feel outrage when algorithms encroach on their profession. They feel many of their predictions do turn out correct and that they have skill, but their downfall is they don’t know the boundaries of their skill.
• It seems more heart-wrenching to lose a child due to an algorithm’s mistake than because of a human error.

But this stigma against algorithms is dissipating as they recommend us useful things to buy and form winning baseball teams.

Antidote to Intuitions

When hiring for a job, Kahneman recommends standardizing the interview:

• Make a list of up to 6 traits important for success in the role. Ideally these are orthogonal traits that don’t overlap strongly with each other.
• Create direct questions to assess each trait. Use as little discretion as possible.
  • If assessing conscientiousness, you might ask, “how many times were you late to work in the past month?”
• Create a rubric from 1 to 5, with notes on what you’re looking for in each grade.
• When interviewing, collect information on one trait at a time, completing it before moving on.
• Finally, hire the person with the highest score, period. Do not override this rule to favor someone else your intuition likes better—you’re letting the halo effect and liking bias override you.

When Can You Trust Human Intuition?

Clearly plenty of people develop skilled intuitions. Chess players do spot meaningful moves; doctors do make correct diagnoses. Within academia, the movement of Naturalistic Decision Making (NDM) puts faith in human intuition.

When can you trust human intuition? Kahneman argues accurate human intuition is developed in situations with two requirements:

• An environment that is sufficiently regular to be predictable, with fast feedback
• Prolonged practice to learn these regularities

Here are a few examples:

• Most people can learn to drive. The input → output relationship is clear and immediate.
• Doctors can learn to diagnose with limited data because they receive fast feedback on the true diagnosis from more testing.

Training can even occur theoretically, through words or thoughts. You can simulate situations and rehearse them in your brain to learn. For example, a young military commander can feel tension when going through a ravine for a first time, because he learned that this scenario invited an ambush from enemies.

To the NDM camp, Kahneman concedes that in situations with clear signals, formulas do not identify new critical factors that humans miss. Humans are efficient learners and generally don’t miss obvious predictors. However, algorithms do win at detecting signals within noisy environments.

In the brain, how do accurate intuitive decisions arise? They first arise from pattern matching in memory - System 1 retrieves a solution that fits the situation. System 2 then analyzes it, modifying it to overcome shortcomings until it seems appropriate. If the solution fails, another solution is retrieved and the process restarts.

When Not to Trust Intuition

Not all supposed experts have real predictive skill. The problem with pundits and stock pickers is that they don’t train in predictable environments. When noise dominates the outcomes and feedback cycles are long, any confidence in the intuition’s validity is largely illusory.

Even worse, there can be “wicked” environments, where you learn the wrong lessons from experience if you influence the outcome. For example, doctor Lewis Thomas felt he could predict typhoid by touching the patient’s tongue. In reality, he carried typhoid on his hands—he was actually causing typhoid by touching the patient’s tongue.

Another sign of untrustworthy intuition is high confidence without good explanation. True experts know the limits of their knowledge and are willing to admit it. In contrast, people who are firmly confident all the time, like pundits on TV, may be hired more for their boisterousness than their accuracy.

How confident you feel about your intuition is not a reliable guide to its validity. You need to learn to identify situations in which intuition will betray you.

For example, you might conflate short-term results with long-term results. A psychiatrist may feel skilled in building short-term rapport with patients and believe she’s doing a great job; but short-term rapport might not correlate strongly with long-term outcomes, which take in many more factors.

Part 3-3: The Objective View

We are often better at analyzing external situations (the “outside view”) than our own. When you look inward at yourself (the “inside view”), it’s too tempting to consider yourself exceptional— “the average rules and statistics don’t apply to me!” And even when you do get statistics, it’s easy to discard them, especially when they conflict with your personal impressions of the truth.

In general, when you have information about an individual case, it’s tempting to believe the case is exceptional, and to disregard statistics of the class to which the case belongs.

Here are examples of situations where people ignore base statistics and hope for the exceptional:

• 90% of drivers state they’re above average drivers. Here they don’t necessarily think about what “average” means statistically—instead, they think about whether the skill is easy for them, then intensity match to where they fit the population.
• Most people believe they are superior to most others on most desirable traits.
• When getting consultations, lawyers may refuse to comment on the projected outcome of a case, saying “every case is unique.”
• Business owners know that only 35% of new businesses survive after 5 years. Despite this, 82% of entrepreneurs put their personal odds of success at 70% or higher, and 33% said their chance of failing was zero!
  • Kahneman tells a story of meeting motel owners who said they bought the motel cheaply because “the previous owners failed to make a go of it.” They seemed blithely indifferent to the circumstances that led the previous owner to fail.
• CEOs make large, splashy mergers and acquisitions, despite research showing a poor track record of such strategies working.

Planning Fallacy

The planning fallacy is a related phenomenon where you habitually underestimate the amount of time and resources required to finish a project.

When estimating for a project, you tend to give “best case scenario” estimates, rather than confidence ranges. You don’t know what you don’t know about what will happen—the emergencies, loss of motivation, and obstacles that will pop up—and you don’t factor in buffer time for this.

Kahneman gives an example of a curriculum committee meeting to plan a book. They happily estimate 2 years for completion of the book. Kahneman then asks the editor how long other teams have taken. The answer is 7-10 years, with 40% of teams failing to finish at all. Kahneman then asks how their team skill compares to the other teams. The answer is Kahneman’s team is below average.

This was an astounding example of how a person may have relevant statistics in her head, but then completely fails to recall this data as relevant for the situation. (The book did indeed take 8 years.)

Furthermore, before Kahneman asked his questions, the team didn’t even feel they needed information about other teams to make their guess! They looked only at their own data situation.

Government projects have a funny pattern of being universally under budget and delayed. (Though there may be an underlying incentive at play here, since projects that are lower cost and shorter time are easier to get approved.)

Antidote to the Inside View

The antidote is similar to the correction for heuristics in the last section:

• Identify the appropriate category the situation belongs in.
• Consider the population distribution for the category. Start with this baseline prediction.
• Use specific information about the case that allows you to adjust from the baseline prediction.

Another technique is to write a premortem: “Imagine that it’s a year from now. We implemented the plan. It was a disaster. Write a history of the disaster.” The premortem has a few advantages:

• As a piece of writing, it avoids the public groupthink that arises from conversation.
• It encourages creative dissent before a project starts, which is normally suppressed when a project begins.

Finally, when evaluating how well a project was executed, reward people who finish according to their original deadlines, not those who finish much earlier or later than planned.

On Optimism and Entrepreneurs

Optimism has a lot of advantages. Optimistic people are happier, recover from setbacks more easily, have greater self-confidence, feel healthier, and live longer. Research suggests optimism is largely genetic (though some psychologists believe it can be learned).

Optimistic people play a disproportionate role in shaping the world. They are the inventors, entrepreneurs, and political leaders. They take risks and seek challenges. They’re talented but are also lucky (luckier than they acknowledge). Their success confirms their faith in their judgment and their ability to control events.

As described above, most founders know the statistics—most startups fail, and the path that yields the higher expected value path is to sell their services to an employer. To forsake the latter path and start a company, you need to be overoptimistic or deluded.

One drawback to optimism is that it encourages people to take outsized risks because they overestimate their chances of success. Data points that support this:

• Of inventors who were told their inventions were destined to fail, half ignored the advice and continued, doubling their original losses.
• More optimistic CEOs (those who own more equity in the company) take excessive risks and lower company performance, compared to CEOs who own less equity.
• Movie studios tend to release big budget movies on the same day (like July 4th) because they ignore the competition—“we’ve got a great story and marketing department, so our film is going to do great.” The real question they should be asking is, “considering the market and what everyone else is doing, how many people will see our film?”
• Because of outcome bias, people who take extraordinary risks and have it work are lauded for their prescience and thus serve as a model for new entrepreneurs. All the failures are forgotten.

Despite the humbling statistics on failure, Kahneman notes that yet there is value in the legions of entrepreneurs who try and fail. They perform a market discovery service, figuring out pockets of opportunity that larger companies can later service. Many companies die as “optimistic martyrs.”

And overall, mixing high optimism with good implementation is a positive trait. It allows endurance through setbacks and belief in what one is doing.

Part 4: Choices | 1: Prospect Theory

Part 4 of Thinking, Fast and Slow departs from cognitive biases and toward Kahneman’s other major work, Prospect Theory. This covers risk aversion and risk seeking, our inaccurate weighting of probabilities, and sunk cost fallacy.

Prior Work on Utility

How do people make decisions in the face of uncertainty? There’s a rich history spanning centuries of scientists and economists studying this question. Each major development in decision theory revealed exceptions that showed the theory’s weaknesses, then led to new, more nuanced theories.

Expected Utility Theory

Traditional “expected utility theory” asserts that people are rational agents that calculate the utility of each situation and make the optimum choice each time.

If you preferred apples to bananas, would you rather have a 10% chance of winning an apple, or 10% chance of winning a banana? Clearly you’d prefer the former.

Similarly, when taking bets, this model assumes that people calculate the expected value and choose the best option.

This is a simple, elegant theory that by and large works and is still taught in intro economics. But it failed to explain the phenomenon of risk aversion, where in some situations a lower-expected-value choice was preferred.

Consider: Would you rather have an 80% chance of gaining $100 and a 20% chance to win $10, or a certain gain of $80?

The expected value of the former is greater (at $82) but most people choose the latter. This makes no sense in classic utility theory—you should be willing to take a positive expected value gamble every time.

Risk Aversion

To address this, in the 1700s, Bernoulli argued that 1) people dislike risk, and that 2) people evaluate gambles not based on dollar outcomes, but on their psychological values of outcomes, or their utilities.

Bernoulli then argued that utility and wealth had a logarithmic relationship. The difference in happiness between someone with $1,000 and someone with $100 was the same as $100 vs $10. On a linear scale, money has diminishing marginal utility.

This concept of logarithmic utility neatly explained a number of phenomena:

• This meant that $10 was worth more to someone with $20 than to someone with $200. This aligns with our intuition - people with more money are less excited than poorer people about the same amount of money.
• This explained the value of certainty in gamble problems, like the 80% chance question above. On a logarithmic scale for utility, having 100% of $80 was better than having 80% of $100.
• This also explained insurance - people with less wealth were willing to sell risk to the wealthier, who would suffer less relative utility loss in the insured loss.

Despite its strengths, this model presented problems in other cases. Here’s an extended example.

Say Anthony has $1 million and Beth has $4 million. Anthony gains $1 million and Beth loses $2 million, so they each now have $2 million. Are Anthony and Beth equally happy?

Obviously not - Beth lost, while Anthony gained. Yet Bernoulli’s model would argue they end up at the same utility and should be equally happy. Clearly the model is incomplete and can’t explain this.

Now let’s reset the scenario, giving Anthony $1 million and Beth $4 million again. Now we present Anthony and Beth with the following choice:

1. 50% chance of ending with $1 million or 50% chance of ending with $4 million
2. 100% chance of ending with $2 million

To try to explore the thinking yourself, imagine you’re Anthony, and you have $1 million. Which would you choose?

Now clear your head as best you can, and now imagine you’re Beth, with $4 million. Which would you choose?

If you chose different answers, you revealed the weakness in Bernoulli and expected utility theory. Option 1 has an expected value of $2.5 million, while Option 2 has an expected value of $2 million. According to these older theories, Option 2 should win every time.

But in reality, Anthony, with his lower money, is more inclined to choose option 2, while Beth is more likely to choose option 1. Anthony sees the certain doubling of his wealth as attractive, and would rather not leave it to chance that he ends up with no improvement. In contrast, Beth sees the certain loss of half her wealth as very unattractive. She would rather take the gamble to preserve her wealth.

Puzzling with this concept led Kahneman to develop prospect theory.

Prospect Theory

The key insight from the above example is that evaluations of utility are not purely dependent on the current state. Utility depends on changes from one’s reference point. Utility is attached to changes of wealth, not states of wealth. And losses hurt more than gains.

Consider that you probably don’t know your wealth to the nearest hundred, or even the nearest thousand. But the loss of $100—from an overcharge, or a parking ticket—is very acute. Isn’t this odd?

Consider these two problems:

1. You have been given $1,000. Which do you choose:

• 50% chance to win another $1,000 and 50% chance to get $0, or

• Get an additional $500 for sure

1. You have been given $2,000. Which do you choose:

• 50% chance to lose $1,000, and 50% chance to lose $0

• Lose an additional $500 for sure

(Shortform note: If you’re in the fortunate position of having enough wealth so that these numbers aren’t very compelling to you, try multiplying them by 10x or even 100x, to get to a place where you think hard about the outcome.)

Note these are completely identical problems. In both cases you have the certainty of ending with $1,500, or equal chances of having $1,000 or $2,000. Yet you probably chose different answers.

You were probably risk averse in problem 1 (choosing the sure bet), and risk seeking in problem 2 (choosing the chance). This is because your reference points were different - from one point you were gaining, and in the other you were losing. And losses hurt more than gains, so you try to protect yourself against a loss.

Prospect theory seeks to explain all of the above.

Prospect Theory in 3 Points

1. When you evaluate a situation, you compare it to a neutral reference point.

• Usually this refers to the status quo you currently experience. But it can also refer to an outcome you expect or feel entitled to, like an annual raise. When you don’t get something you expect, you feel crushed, even though your status quo hasn’t changed.

2. Diminishing marginal utility applies to changes in wealth (and to sensory inputs).

• Going from $100 to $200 feels much better than going from $900 to $1,000. The more you have, the less significant the change feels.

3. Losses of a certain amount trigger stronger emotions than a gain of the same amount.

• Evolutionarily, the organisms that treated threats more urgently than opportunities tended to survive and reproduce better. We have evolved to react extremely quickly to bad news.

The master image of prospect theory is this:

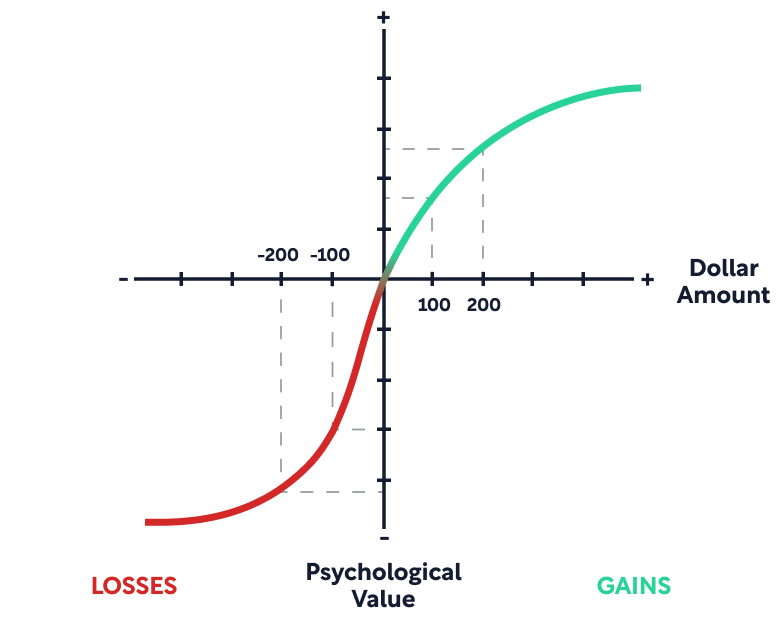
The graph shows how psychological value changes according to the change in dollar amount. The middle of the two axes is the reference point—with no change, there is no psychological value. Psychological value is positive with positive dollar amounts (when you gain money) and negative with negative dollar amounts.

This graph was established through a host of experiments investigating how people perceive gains and losses, and how they trade off decisions like Anthony and Beth above.

Note two important properties of the curve shown:

• Diminishing marginal value: the curve isn’t a straight line on either end. The more money you gain, the less value each increment of money gives you. The same is true of losing money—losing $100 causes less anguish than 10x the anguish of losing $10.
• Loss aversion: the curve on the left of the y-axis has a steeper slope than the curve to the right of the y-axis. This signifies that the psychological pain of losing $100 is greater in intensity than the joy in gaining $100. Losses hurt more than gains do.

People have different curves, depending on their sensitivity to loss aversion. The ratio of slopes is called the “loss aversion ratio.” For most people, the ratio ranges between 1.5 to 2.5 - people would have to gain $200 to offset a loss of $100. In contrast, professional risk takers, like stock traders, are more tolerant of losses and have a lower loss aversion ratio, possibly because they have psychologically adapted to large fluctuations.

Revisiting Bernoulli’s Conundrum

Let’s revisit the scenario with Anthony and Beth. Anthony has $1 million and Beth has $4 million. They both have the following choices:

1. 50% chance of ending with $1 million or 50% chance of ending with $4 million
2. 100% chance of ending with $2 million

Anthony chooses the option 2, while Beth chooses option 1.

Prospect Theory now explains why. From the curve above, see that:

• For gains, 100% of 100 is larger than 50% of 200, because of how the curve flattens with more money. People are risk averse to get gains. Anthony would rather lock in a certain gain than risk getting nothing.
• For losses, 50% of -200 is less negative than 100% of -100. People are risk seeking to avoid losses. Beth would rather risk losing more if there’s a chance she keeps her money, than to have a certain loss.

While Bernoulli presented utility as an absolute logarithmic scale starting from 0, prospect theory calibrates the curve to the reference point. People feel differently depending on whether they’re gaining or losing money.

Part 4-2: Implications of Prospect Theory

With the foundation of prospect theory in place, we’ll explore a few implications of the model.

Probabilities are Overweighted at the Edges

Consider which is more meaningful to you:

• Going from 0% chance of winning $1 million to 5% chance
• Going from 5% chance of winning $1 million to 10% chance

Most likely you felt better about the first than the second. The mere possibility of winning something (that may still be highly unlikely) is overweighted in its importance . (Shortform note: as Jim Carrey’s character said in the film Dumb and Dumber , in response to a woman who gave him a 1 in million shot at being with her: “ so you’re telling me there’s a chance! ”)

More examples of this effect:

We fantasize about small chances of big gains.

• Lottery tickets and gambling in general play on this hope.
• A small sliver of chance to rescue a failing company is given outsized weight.

We obsess about tiny chances of very bad outcomes.

• The risk of nuclear disasters and natural disasters is overweighted.
• We worry about our child coming home late at night, though rationally we know there’s little chance anything bad happened.

People are willing to pay disproportionately more to reduce risk entirely.

• Parents were willing to pay 24% more per bottle of insect spray to reduce a child’s risk of poisoning by 2/3, but they were willing to pay 80% as much to reduce it to 0.
• People are not willing to pay half price for insurance coverage that covers you only on odd days. Technically, this is a good deal, because there are more odd days in a year than even, so you’re getting more value for your money. But the reduction from 100% risk to 50% risk is far less valuable than the reduction from 50% risk to 0% risk.

We Feel Better About Absolute Certainty

We’ve covered how people feel about small chances. Now consider how you feel about these options on the opposite end of probability:

• In a surgical procedure, going from 90% success rate to 95% success rate.
• In a surgical procedure, going from 95% success rate to 100% success rate.

Most likely, you felt better about the second than the first. Outcomes that are almost certain are given less weight than their probability justifies. 95% success rate is actually fantastic! But it doesn’t feel this way, because it’s not 100%.

As a practical example, people fighting lawsuits tend to take settlements even if they have a strong case. They overweight the small chance of a loss.

(Shortform note: how we feel about 0% and 100% are similar and are inversions of each other. A 100% gain can be converted into 0% loss—we feel strongly about both. For example, say a company has a 100% chance of failure, but a new project reduces that to 99%. It feels as though the chance of failure is reduced much more than 1%. Inversely, a project that increases the rate of success from 0% to 1% seems much more likely to work than 1% suggests.)

How We Feel About Probabilities

The above points give a feel for how people feel about probabilities, but let’s be specific. Here’s a chart showing the weight that people give each probability:

At the two extremes, people feel how you would expect—at 0% probability, people weigh it at 0; at 100% probability, people weigh at 100.

But in between, there are interesting results:

• The weight for 1% is 5.5 (when it should rationally be 1.0) and the weight for 99% is 91.2 (far from 99). People overestimate low probabilities, and they discount high probabilities that aren’t certain.
  • Imagine that you’re told there’s a 99% chance your operation will be successful, with a 1% rate of permanent disability. You will certainly be more anxious than the miniscule 1% suggests!
• Note that 50% is weighted at 42.1.
  • Imagine that you have a 50-50 coin toss where heads wins you a dollar, tails loses you a dollar. You really would not value this as a 50-50 coin toss—you feel the possibility of a loss more strongly than the gain.
• The range between 5% and 95%, which covers 90% in probability, ranges in weight from 13 to 79, covering just 66 points. This means we are not adequately sensitive to changes in probability.
  • Similarly, we can’t easily tell the difference between a 0.001% cancer risk and 0.00001% risk, even though this translates to 3000 cancers for the US population vs 30.

The Fourfold Pattern of Prospect Theory

Putting prospect theory into another summary form, here’s a 2x2 grid showing how people feel about risk in different situations. The upper left quadrant shows how people feel about a high probability of a gain, the upper right shows how people feel about a high probability of a loss, and so on.

Putting it all together - two factors are at work in evaluating gambles:

• Diminishing sensitivity, so that more of the same causes less of a change in psychological value (in the graph, the slope decreases as you move further from the y-axis)
• Inaccurate weighting of probabilities at the edges

In the first row of this table, the two factors work in the same direction:

• In the upper right quadrant, diminishing sensitivity causes loss aversion: a sure loss is painful. On the prospect theory graph, 100% of -900 is more negative than 90% of -1,000.
• Making matters worse is the inaccurate weighting of probabilities. While 100% is weighted at 100, 90% is weighted only at 71. This certainty effect causes the 100% loss to feel much more painful than a very high chance of loss.
• Similarly, in the positive situation on the upper right, the diminishing sensitivity makes a certain lower gain more attractive, and the certainty effect reduces the attractiveness of the gamble.

In the bottom row, the two factors work in opposite directions :

• In the lower left corner, diminishing sensitivity still makes the sure gain more attractive than the chance of a gain. But the overweighting of low probabilities overcomes this effect, so people in this quadrant tend to choose the 5% gamble.

Kahneman notes that many human tragedies happen in the upper right quadrant. People who are between two very bad options take desperate gambles, accepting a high chance of making things worse to avoid a certain loss. The certain large loss is too painful, and the small chance of salvation too tempting, to decide to cut one’s losses.

Miscellaneous Implications

Opposing Incentives in Litigation

Litigation is a nice example of where all of the above can cause tumult:

• Plaintiffs file frivolous lawsuits. They have a low chance of winning, and they overweight the probability of winning (lower left corner in the fourfold pattern).
• Defendants prefer settling frivolous lawsuits to lower the risk of a more expensive loss (lower right corner). Yet if the defendant does this habitually for each lawsuit, it invites more frivolous lawsuits, and can thus be costly in the long run.

We can also reverse the situations:

• A plaintiff has a strong case and has an almost certain chance to win, but wants to avoid the small chance of a loss. She is prone to risk-aversively take a settlement (upper left corner).
• The defendant knows she’s likely to lose, but has a small chance of winning. She’s willing to drag the case on, because the certain loss from a settlement with the plaintiff is painful and the small chance of winning is gratifying (upper right corner).
• In this case, the defendant holds the stronger hand, and the plaintiff will settle for less than the case strength suggests.

Theory-Accepted Blindness

Why did it take so long for someone to notice the problems with Bernoulli’s conception of utility? Kahneman notes that once you have accepted a theory and use it as a tool in your thinking, it is very difficult to notice its flaws . Even if you see inconsistencies, you reason them away, with the impression that the model somehow takes care of it, and that so many smart people who agree with your theory can’t all be wrong.

In Bernoulli’s theory, even when people noticed inconsistencies, they tried to bend utility theory to fit the problem. Kahneman and Tversky instead made the radical choice to abandon the idea that people are rational decision-makers, and instead took a psychological bent that assumed foibles in decision-making.

Blind Spots in Prospect Theory

Prospect theory has holes in its reasoning as well. Kahneman argues that it can’t handle disappointment - that not all zeroes are the same. Consider two scenarios:

1. 1% chance to win $1 million and 99% chance to win nothing
2. 99% chance to win $1 million and 1% chance to win nothing.

In both these cases, prospect theory would assign the same value to “winning nothing.” But losing in case 2 clearly feels worse. The high probability of winning has set up a new reference point—possibly at say $800k.

Prospect theory also can’t handle regret, in which failing to win a line of gambles causes losses to become increasingly more painful.

People have developed more complicated models that do factor in regret and disappointment, but they haven’t yielded enough novel findings to justify the extra complexity.

Part 4-3: Variations on a Theme of Prospect Theory

Indifference Curves and the Endowment Effect

Basic theory suggests that people have indifference curves when relating two dimensions, like salary and number of vacation days. Say that you value one day’s salary at about the same as one vacation day.

Theoretically, you should be willing to trade for any other portion of the indifference curve at any time. So when at the end of the year, your boss says you’re getting a raise, and you have the choice of 5 extra days of vacation or a salary raise equivalent to 5 days of salary, you see them as pretty equivalent.

But say you get presented with another scenario. Your boss presents a new compensation package, saying that you can get 5 extra days of vacation per year, but then have to take a cut of salary equivalent to 5 days of pay. How would you feel about this?

Likely, the feeling of loss aversion kicked in. Even though theoretically you were on your indifference curve, exchanging 5 days of pay for 5 vacation days, you didn’t see this as an immediate exchange.

As with prospect theory, the idea of indifference curves ignores the reference point at which you start. In general, people have inertia to change.

They call this the endowment effect. Before you have something, you might have a certain indifference curve. But once you get it, a new reference point is set, and from this point loss aversion sets in—the utility of a gain is less than a corresponding loss.

Here are a few examples of when people overvalue things once they own it:

• Sometimes you’re only willing to sell something for higher than you can buy it on the market (like a collector’s item).
• Famous experiment: half of the subjects were given mugs and were asked to quote prices to sell their mug; the other half, who were not given mugs, were asked to bid for the cups. The buyers had an average bid of $2.87; the cup owners quoted $7.12, over double the buyers’ bid! Note that the cup owners had just received their cups a few minutes earlier.
  • Notably, a third group (Choosers) could either receive a mug or a sum of money, and they indicated that receiving $3.12 was as desirable an option as receiving the mug. It’s important to note that the mug owners had been given an essentially identical choice: they were either going to leave with the mug or with the money someone paid for it. But because they already possessed the mug, they vastly embellished their ask.
• Owners who buy a house at higher prices spend longer trying to sell their home and set a higher listing price - even though the current market value is rationally all that matters.

The endowment effect doesn’t occur in all cases - people are willing to exchange $5 for five $1 bills, and furniture vendors are happy to exchange a table for money. When the asset under question is held for exchange, the endowment effect doesn’t apply.

You only feel endowed with items that are planned for consumption or use, like a bottle of wine or vacation days.

As with prospect theory and loss aversion, experienced financial traders show less attachment to the endowment effect.

Goals are Reference Points

We are driven more to avoid failing a goal than to exceed it. Failing a goal is perceived as a loss; exceeding the goal is a gain.

Examples:

• Studies of cab drivers show they have a daily target income. When the going is good on a particular day, they clock out early, rather than making the most of the day to offset less profitable days.
• Golfers are more accurate when they putt for par (to avoid a bogey, or one over par) than when they aim for a birdie (one under par). The difference in success is 3.6%.

Status Quo Bias

In another reframing of loss aversion, we are biased toward keeping the status quo. Two effects are at play here: 1) the endowment effect exaggerates the value of what you have, warping your prior indifference curve, and 2) loss aversion makes you hesitant to take on risky bets, since losses are more painful than gains.

Examples:

• In negotiations, concessions are painful because they represent losses from the status quo. Both parties are trying to make concessions, but because losses outweigh gains, the concessions from the other side don’t make up for your personal concessions. This is why negotiations can end up feeling like everyone walks away unhappy. This feeling is aggravated in situations where parties are merely allocating losses, like an ailing company negotiating with a labor union on how to cut staff, instead of negotiating to split a growing pie.
• Political reform is difficult because the people who have something to lose mobilize more aggressively than those who win. Reforms thus often include grandfather clauses that protect existing stakeholders.

Fairness

The normal price of a good in a store is the reference point. Generally, it’s considered unfair to exploit market power to increase prices to match increased demand, unless the store must do so to retain profits. This is why there’s outrage when a supermarket in a blizzard suddenly raises prices on shovels.

Consider this scenario about pay: an employee is hired at $9 per hour, but the market rate drops to $7 per hour. It’s considered unfair to change the employee’s rate. But if that employee leaves, it’s acceptable to pay the new employee $7 per hour. Intuitively this sounds right, but rationally it sounds odd. The market rate should be the market rate.

• The explanation: the old employee had a personal entitlement to the wage. The new employee has no entitlement to the previous worker’s wage. On the other side, the company has entitlement to retain its current profit, but not to increase it by encroaching on others’ entitlements. These are intuitive notions of fairness that aren’t often made explicit.

Employers who violate rules of fairness are punished by reduced productivity by employees and sales by customers.

(Shortform note: the rise of on-demand services like Uber and real-time pricing may blunt this effect over time, gradually educating the public about supply, demand, and pricing. Soon it might seem normal for shovels to be more expensive during snowstorms.)

Regret and Responsibility

In another twist, the feeling of regret depends on your default action and whether you deviate from it. If you do something uncharacteristic and fail, you’re more likely to feel regret, but others are less likely to blame you.

Consider: Alan never picks up hitchhikers. Yesterday he gave a man a ride and was robbed.

Barry frequently picks up hitchhikers. Yesterday he gave a man a ride and was robbed.

Who will experience greater regret?

Who will be criticized most severely by others?

Common answer: Alan will experience greater regret, but Barry will be criticized most severely. Alan will have wished he stayed the normal path and would want to undo the event. Barry will be seen as habitually taking unreasonable risks, and thus “deserving of his fate.”

(Shortform note: sadly, this might drive some people to blame victims of rape, who allegedly were “asking for it” through their typical dress or behavior.)

In some cases, the default option is to do nothing to avoid regret (e.g. not sell your stock), while the alternative unusual action is to do something.

Corollaries

If you do the normal thing and get a bad outcome, this feels better than doing the unusual thing and getting a bad outcome.

• Selling stock X and missing out on stock X’s big gain feels worse than keeping stock X and missing out on a different stock Y’s big gain.
• Volunteering for a clinical trial and getting a disease from that trial feels much worse than just living and getting the same disease.

If you do an unusual thing and get a good outcome, this feels better than doing a normal thing and getting a good outcome.

• People are happier if they gamble and win, than if they refrain from the gamble and get the same amount.

If you anticipate a bad outcome and regret, you will tend to do the normal thing.

• Consumers at a store who are reminded they may feel regret over their purchase tend to favor brand names over generics.
• A surgeon may believe an experimental treatment is better for a patient but is more liable for a bad outcome than if she were to follow protocol. This anticipation of regret and punishment may lead the surgeon to take the less optimal treatment.
• For employees who wish to start a company and strike out on their own, picturing their startup failing will hold people into staying in their salaried jobs.

If you anticipate a good outcome, you will tend to do the unusual thing.

Taboo tradeoff: there are certain things that people hold as sacrosanct (notably, health and safety), against which they would be unwilling to trade anything. This is driven by the prediction of strong regret if they made the trade and harm were to have resulted.

• The governments of Europe use the “precautionary principle,” which prohibits any action that might cause harm. This overly cautious principle could have precluded innovations like airplanes, antibiotics, and X-rays.

The risk of regret is that it causes inappropriate loss aversion. (Shortform note: this is aggravated by two factors we’ve previously discussed: 1) because probabilities are overweighted at the edges, we overestimate low chances of harm, 2) loss aversion makes the losses feel more painful than the gains.)

Antidotes to Regret

As you journal your decisions, note the possibility of regret before deciding. Then if a bad outcome happens, remember that you considered the possibility of regret before you made your decision. This avoids the hindsight bias and the feeling of “I almost made a better choice and I should have known better.”

Downweight your future regret—in practice, even in the case of a bad outcome, you will deploy psychological defenses to soothe this pain.

Specificity and Emotion

When an event is made specific or vivid, people become less sensitive to probability (lower chances are overestimated and higher chances are underestimated).

When an event is specifically defined, your mind constructs a plausible scenario in which it can happen. And because the judgment of probability depends on the fluency to which it comes to mind, you overestimate the probability. On the other side of the spectrum, the possibility of its not occurring is also vivid, and thus overweighted.

Here are a few examples of how specificity decreases sensitivity to probability:

• People were asked to estimate the chances that each of 8 NBA playoffs teams had in winning the championship. The sum of chances for all teams should of course total 100%. But for these subjects, the sum was 240%! The reason: when considering each team in isolation, it was easy to construct a plausible path to winning, while the alternative of (7 other teams) was a diffuse possibility. Thus each individual team’s chances was overestimated, when the attention was focused on that team.
  • This effect disappeared when the scenario was simplified, and subjects were asked to estimate the chance of the winning team coming from the Eastern vs the Western conference. In this case, the event and its alternative were equally specific, and it was clearer that the probabilities should add to 100%.
• This partially explains the planning fallacy. The successful case is very available to the mind, so its likelihood is embellished. The many failure cases are diffuse and not concentrated on.
• People become less sensitive to probability when the outcomes are emotional (like “getting a painful shock” or “kissing your celebrity crush”) rather than cash-based.
• When people buy lottery tickets, they tend to bask in the fantasy of winning. This may make them less sensitive to the probability of winning.
• (Shortform example: In cognitive behavior therapy for mental illness, patients are instructed to picture instances when they were competent. Making this vivid allows a depressed patient to increase their estimation of competence.)

(Shortform note: this effect could be the foundation of the common advice to visualize your success. Doing so helps you overcome the statistical knowledge of the low rate of success, which would otherwise drag you down psychologically.)

Denominator Neglect

Each rate or probability is a fraction, consisting of a numerator at the top (the events you are estimating) and a denominator (all the possible events).

Denominator neglect occurs when people focus on the size of the numerator, rather than examining the basal rate.

Here’s an example:

You have the choice of drawing a marble from one of two urns. If you draw a red marble, you win a prize.

• Urn A contains 10 marbles, of which 1 is red and the rest are white.

• Urn B contains 100 marbles, of which 8 are red and the rest are white.

Which do you choose?

30% of subjects choose Urn B, since it has a larger number of marbles. Before you think this is silly, imagine a picture of both urns. Urn A has just 1 winning marble among other white marbles. In contrast, Urn B has 8 winning chances, standing out among the white marbles. Urn B conveys a more hopeful feeling.

Here are more examples of denominator neglect:

• Percentages and fractions are mathematically equivalent, but one is more impactful than the other. A 0.001% of permanent disability seems low. On the other hand, “one out of 100,000 children will be disabled” seems high. In the latter description, the other 99,999 children have faded into the background—the focus is on the one child who gets disabled.
• Manipulation of the fraction also makes a difference. People who read about “a disease that kills 24 people out of 100” rated it less dangerous than people who read about “a disease that kills 1,286 people out of every 10,000.” The first disease is actually nearly twice as deadly, but the second numerator is much larger and thus looks more dangerous.
  • (Note that this study was a between-subjects study, in that one group saw one presentation and gave a rating, and another group saw the other presentation. Prompting a direct comparison within one person would invoke System 2 and likely cause less error.)

Antidotes to Specificity and Denominator Neglect

(Shortform note: the following are our additions and not explicitly described in the book.)

• When estimating the chances of a project working, also picture the failure cases vividly and estimate their probabilities. This will counteract the vividness of the success case.
• When you hear a vivid story about how things will work, strip away the irrelevant details to regain sensitivity to probabilities.
• To avoid denominator neglect, always reduce two statistics to the same denominator for comparison. For instance, if given two fractions, 3 out of 100 and 400 out of 10,000, convert them both to a denominator of 10,000. Compare apples to apples.

In some cases, you might exploit these biases for your own gain to overcome your hesitation:

• If you’re hesitant because you know you have a small chance of success (like starting a new business), paint a vivid picture of the success you could enjoy. This will help you overestimate the chances of success. (Though use this with caution, because you might not want to delude yourself too much.)
• If you’re facing a bad outcome that is likely, then think about the good outcome and make it more vivid. This will help counteract the vividness of the bad outcome. For instance, if you’re suffering from cancer and are afraid that your chemo treatment won’t work, picture the inverse event of being cured and celebrating your grandson’s birthday.
• To embellish the risk of a number, make the denominator large and focus on the numerator. To make a risk look less dangerous, make the denominator small and focus on the percentage.

Part 4-4: Broad Framing and Global Thinking

When you evaluate a decision, you’re prone to focus on the individual decision, rather than the big picture of all decisions of that type. A decision that might make sense in isolation can become very costly when repeated many times.

Consider both decision pairs, then decide what you would choose in each:

Pair 1

1) A certain gain of $240.

2) 25% chance of gaining $1000 and 75% chance of nothing.

Pair 2

3) A certain loss of $750.

4) 75% chance of losing $1000 and 25% chance of losing nothing.

As we know already, you likely gravitated to Option 1 and Option 4.

But let’s actually combine those two options, and weigh against the other.

1+4: 75% chance of losing $760 and 25% chance of gaining $240

2+3: 75% chance of losing $750 and 25% chance of gaining $250

Even without calculating these out, 2+3 is clearly superior to 1+4. You have the same chance of losing less money, and the same chance of gaining more money. Yet you didn’t think to combine all unique pairings and combine them with each other!

This is the difference between narrow framing and broad framing. The ideal broad framing is to consider every combination of options to find the optimum. This is obviously more cognitively taxing, so instead you use the narrow heuristic—what is best for each decision at each point?

An analogy here is to focus on the outcome of a single bet, rather than assembling a portfolio of bets.

Yet each single decision in isolation can be hampered by probability misestimations and inappropriate risk aversion/seeking. When you repeat this single suboptimal decision over and over, you can rack up large costs over time.

Practical examples:

• If given a highly profitable gamble (e.g. 50-50 to lose 1x or gain 1.5x), you may be tempted to reject the gamble once. But you should gladly play 100 times in a row if given the option, for you are almost certain to come out ahead.
• In a company, individual project leaders can be risk averse when leading their own project, since their compensation is heavily tied to project success. Yet the CEO overlooking all projects may wish that all project leaders take on the maximum appropriate risk, since this maximizes the expected value of the total portfolio.
• The opposite scenario may also happen: in a company, leaders of individual projects that are failing may be tempted to run an expensive hail-mary, to seek the small chance of a rescue (because of overweighting probabilities at the edges). In the broad framing, the CEO may prefer to shut down projects and redirect resources to the winning projects.
• A risk-averse defendant who gets peppered with frivolous lawsuits may be tempted to settle each one individually, but in the broad framing, this may be costly compared to the baseline rate at which it would win lawsuits (let alone settling lawsuits invites more lawsuits).
• Appliance buyers may buy individual appliance insurance, when the broad framing of all historical appliances may show this is clearly unprofitable for individuals.

Antidote to Narrow Framing

To overcome narrow framing, adopt risk policies: simple rules to follow in individual situations that give a better broad outcome. Examples:

• Check your stocks only once a quarter. Don’t trade on emotion.
• Always take the highest possible deductible for insurance.
• Never buy extended warranties.
• (Shortform suggestions: treat your time as costing $X per hour. Avoid spending time on activities that are unprofitable at this rate, even if you have a sunk cost.
• Always prioritize projects by return on investment (ROI) or internal rate of return (IRR), not by other confounding reasons.)
• You win a few, you lose a few. Don’t obsess over any individual outcome.

Mental Accounts and Sunk Costs

Related to narrow framing - we have a tendency to bin outcomes into separate accounts. This provides organization and simplifies calculations, but can become costly. People don’t like to close accounts with a negative balance.

Examples of when binning is harmful:

• Novice stock traders see each stock in isolation, selling to capture gains and keeping losers to recover losses, when the opposite is a more profitable strategy. Experienced stock traders have the broader framing that the portfolio of stocks is more important than any individual stock.
• Sunk cost fallacy occurs when you focus on the item at hand, rather than a global view of all assets and possibilities.
  • For example, someone who buys a movie ticket is more willing to drive through a snowstorm to see the movie, compared to someone who was gifted the ticket. If the first person were willing to broaden the framing beyond the single ticket to include the other uses of his time, he might make a different decision.
• In companies, a CEO who has made sunk costs unsuccessfully is often replaced. The new CEO is unencumbered by the mental accounting and can objectively cut losses.

Binning isn’t always harmful. Here are examples of when keeping separate accounts might be helpful:

• People tend to bucket their money into separate financial accounts, such as spending, savings, investment, retirement, and emergency funds. Theoretically, you could simply use one giant account, but this may invite problems with self-control and spending.
• Golfers who putt more accurately to avoid bogey than to get a birdie keep a separate mental account of each hole, rather than considering the overall score. In some ways, this might be helpful to overcome the psychological drain of performing poorly that day.

Reversals

Because of a narrow frame, System 1 doesn’t know what information it’s missing. It doesn’t consider the global set of possibilities and make decisions accordingly. This can lead to odd situations where you make one set of decisions when considering two cases individually, then a contradictory decision when you consider them jointly.

Consider a nonprofit that reduces plastic in the ocean to avoid poisoning and killing baby dolphins. How much are you willing to donate to support the cause?

Now consider the discovery that farmers are at significantly higher risk of skin cancer because of the time they spend outdoors. How much are you willing to donate to a nonprofit that reduces cancer for at-risk groups?

You are likely more willing to pay a higher amount for the dolphins than the farmers. In isolation, each scenario engages a different “account” and intensity of feeling. Saving baby dolphins employs the “save the animals” account, and baby dolphins is high on the scale (relative to saving wasps). You intensity match the high emotion you feel to an amount you’re willing to pay.

In contrast, the farmer skin cancer example evokes a “human public health” account, in which farmer skin cancer is likely not as high a priority as baby dolphins is on the saving animals account. Emotion is lower on this account, so the donation is lower.

Now consider the two examples together. You have the option of donating to a dolphin-saving non-profit, or a human cancer-reducing non-profit. Which one are you more willing to pay for? Likely you now realize that humans are more important than animals, and you recalibrate your donations so the second amount exceeds the first.

Judgment and preferences are coherent within categories, but may be incoherent when comparing across categories.

And because of the “what you see is all there is” bias, alternative categories may not be available for you to consider. Much of life is a between-subjects trial - we only get exposed to one major event at a time, and we don’t think to compare across instances.

Problems can arise when you don’t have a clear calibration of a case to the global set of cases. Examples:

• Rulings for court cases can be miscalibrated across the judicial system. When considered in isolation, a court case involving a poisoned child is assigned a lower judgment than a case involving embezzlement of $10 million. When considered jointly, the poisoned child amount exceeds $10 million, since there is now an anchor. Yet in the US legal system, jurors are not allowed to consider other cases when assessing damages, so this miscalibration may not be easily corrected.
• Government agency fines make sense within the context of the agency, but are inconsistent between agencies. A worker safety fine may be $7k, while a wild bird conservation violation may cost $25k.
• (Shortform example: salespeople typically compare what they’re selling to poorer alternatives, but they omit superior alternatives or entirely different ways to spend your money that might be better.)
• (Shortform example: when reducing spending, keeping separate accounts can lead to disproportionate attention. In the “coffee” account, reducing spend by $200/year seems like a big win, since the base is low. But the bigger absolute savings might be in reducing rent by moving to a smaller house, which might save $5,000/year.)

Antidotes to Narrow Framing and Reversals

(Shortform note: the following are our additions and not explicitly described in the book.)

• Reduce all decisions down to a single fungible metric, in the broadest account possible, to allow global calibration.
  • Decisions around human life can be assessed in terms of a single metric like Quality-adjusted life years per $. This way, repairing glaucoma can be compared to childhood cancers.
  • Projects and investments should be considered in terms of ROI or rate of return, so that all possible spending can be assessed on the same scale from a global account.
  • Personal decisions can be considered in terms of happiness per $ or per hour.
• Deliberately consider the broad range of alternatives for scarce resources, such as time, labor, and money. Define the global set of opportunities, rather than focusing on the narrow account.

Framing Effects

The context in which a decision is made makes a big difference in the emotions that are invoked and the ultimate decision. In particular, even though a gain can be logically equivalently defined as a loss, because losses are so much more painful, the decisions may be contradictory.

Consider how enthusiastic you are about each opportunity:

• A 10% chance to win $100, and a 90% chance to lose $5.

• Buying a $5 raffle ticket that gives you a 10% chance to win $105 and a 90% chance of winning nothing.

These are logically identical situations - yet the latter opportunity is much more attractive! Loss aversion is at play here again. Losses are more painful than uncaptured gains.

Even though framing makes a large difference, most of us accept problems as they are framed, without considering alternative framings.

Consider two framings of two vaccine programs that can save 600 people affected by a virus:

• Program A will save 200 people. Program B has ⅓ chance of saving 600 and ⅔ chance of saving none.

• Program A will leave 400 people dead. Program B has ⅓ chance that nobody will die, and ⅔ chance that 600 will die.

Per prospect theory, you can predict that people prefer A in the first set and B in the second set. But again, these framings are logically equivalent.

Consider which is better for the environment:

• Adam switches from a car with 12mpg to a car with 14mpg.

• Barry switches from a car with 30mpg to a car with 40mpg.

Barry’s move looks like a bigger jump (10mpg and 33% jump) but this is deceptive. If they both drive the same distance in a year, Adam will use 119 fewer gallons of gas, whereas Beth will cut her use by only 83 gallons. Rather than miles per gallon, the real metric that matters is gallons per mile, which inverts the mpg, and differences in fractions are less intuitive.

For an extreme, consider going from 1mpg to 2mpg vs 100mpg to 200mpg. Over 1000 miles, the former will save 500 gallons; the latter, only 5!

Here are more examples of how framing leads to distorted interpretations:

• A medical procedure with a 90% chance of survival sounds more appealing than one with a 10% chance of mortality.
• If the real price of a good is $20, then selling it as $10 off a $30 good sounds better than a $5 surcharge to a $15 good.
• In a sports game, saying something like “the Patriots lost” evokes different feelings than “the Rams won,” even though these two are logically equivalent.
• For organ donors, changing from an opt-in to an opt-out can increase donation rates from 10% to 90%. When action is required to overcome the default, a lazy System 2 finds it easier to follow the default.

Even experts like doctors and public health officials suffer from the same framing biases. Even more troubling, when presented with the inconsistency, people cannot explain the moral basis for their decisions. System 1 used a simple rule—saving lives is good, deaths are bad—but System 2 has no moral rule to easily solve the question.

Conclusions of Prospect Theory

We’ve shown that humans are not rational in the decisions they make. Unfortunately, when society believes in human rationality, it also promotes a libertarian ideology in which it is immoral to protect people against their choices. “Rational people make the best decisions for themselves. Who are we to think we’re better?” This leads to beliefs like:

• People know what they’re doing when they choose not to save for retirement or eat to obesity.
• People who are addicted are rational agents who strongly prefer immediate gratification and accept future addiction as a consequence.

This belief in rationality also leads to a harsher conclusion: people apparently deserve little sympathy for putting themselves in worse situations. Elderly people who don’t save get little more sympathy than people who complain about a bill after ordering at a restaurant. Rational agents don’t make mistakes.

Behavioral economists believe people do make mistakes and need help to make more accurate judgments. They believe freedom is a virtue worth having, but it has a cost borne by individuals who make bad choices (that are not completely their fault) and by a society that feels obligated to help them.

The middle ground might be libertarian paternalism, in which the state nudges people to making better decisions and give the freedom for people to opt out. This includes nudges for retirement savings, health insurance, organ donation, and easy-to-understand legal contracts.

Part 5-1: The Two Selves of Happiness

Part 5 of Thinking, Fast and Slow departs from cognitive biases and mistakes and covers the nature of happiness.

(Shortform note: compared to the previous sections, the concepts in this final portion are more of Kahneman’s recent research interests and are more a work in progress. Therefore, they tend to have less experimental evidence and less finality in their conclusions.)

Happiness is a tricky concept. There is in-the-moment happiness, and there is overall well being. There is happiness we experience, and happiness we remember.

Consider having to get a number of painful shots a day. There is no habituation, so each shot is as painful as the last. Which one represents a more meaningful change?

• Decreasing from 20 shots to 18 shots
• Decreasing from 6 shots to 4 shots

You likely thought the latter was far more meaningful, especially since it drives more closely toward zero pain. But Kahneman found this incomprehensible. Two shots is two shots! There is a quantum of pain that is being removed, and the two choices should be evaluated as much closer.

In Kahneman’s view, someone who pays different amounts for the same gain of experienced utility is making a mistake. This thought experiment kicked off Kahneman’s investigation into happiness.

Experiencing Self vs Remembering Self

Kahneman presents two selves:

• The experiencing self: the person who feels pleasure and pain, moment to moment. This experienced utility would best be assessed by measuring happiness over time, then summing the total happiness felt over time. (In calculus terms, this is integrating the area under the curve.)
• The remembering self: the person who reflects on past experiences and evaluates it overall.

The remembering self factors heavily in our thinking. After a moment has passed, only the remembering self exists when thinking about our past lives. The remembering self is often the one making future decisions.

But the remembering self evaluates differently from the experiencing self in two critical ways:

• Peak-end rule: The overall rating is determined by the peak intensity of the experience and the end of the experience. It does not care much about the averages throughout the experience.
• Duration neglect: The duration of the experience has little effect on the memory of the event.

Both effects operate in classic System 1 style: by averages and norms, not by sums.

This leads to preferences that the experiencing self would find odd, and show that we cannot trust our preferences to reflect our interests.

In the ice water experiment, participants were asked to stick their hand in cold water, then to evaluate their experience. Participants stuck their hand in cold water in two episodes: 1) a short episode: 60 seconds in 14°C water, and 2) a long episode: 60 seconds in 14°C, plus an additional 30 seconds, during which the temperature increased to 15°C. They were then asked which they would repeat for a third trial.

The experiencing self would clearly consider the long episode worse—you’re suffering for more time. But the longer episode had a more pleasant end.

Counter-intuitively, 80% of participants preferred the long episode, thus, in Kahneman’s view, suffering “30 seconds of needless pain.” They picked the option they liked more.

Oddly, people would prescribe the shorter episode for others, since they care about the experiencing self of others. But when thinking about themselves, they care more about the remembering self.

More examples of oddities with the remembering self:

• Would you take a vacation that was very enjoyable, but at the end you took a pill that gave you total amnesia of the event? Most would decline, suggesting that memories are a key, perhaps dominant, part of the value of vacations. The remembering self, not the experiencing self, chooses vacations!
• Inversely, you have two options for an operation: 1) you undergo general anesthesia, but will endure a month of mild pain after; 2) you remain conscious and feel intense pain, but are given amnesia to remove any memory of the episode.
  • Many prefer #2, indifferent to the pains of their experiencing self. It’s as though you are only your remembering self, and the experiencing self (who actually does the living) is a stranger.
• We can enjoy a movie all the way throughout, but if the ending is poor or interrupted, we have a worse impression.
• In general, we favor peak highs with short duration, rather than moderate highs over long duration. (Shortform note: this includes intense sensations like roller coasters and perhaps use of narcotic drugs.)
• The end of someone’s life tends to matters a lot more than duration. For someone who dies at age 57, you don’t care as much if they lived a whole extra year to age 58. But you do care about whether she was surrounded by her family in her last 10 minutes, or whether she was alone.
  • Similarly, In an experiment, people were told of Jen, an extremely happy person throughout life who died painlessly at 60 in an accident. Another group was told of a similar Jen who lived to 65, with the first 60 years equally happy as the first Jen, but with the last 5 years being slightly less pleasant. The 5 only “slightly happy” years caused a drop in perceived total happiness in that life. Again, this is System 1 caring more about averages than summing the total experienced happiness.
• After a person dies, we feel moved by changes to their stories that they clearly did not experience.
  • A man may have died happily believing his wife was faithful, only for us to find out postmortem that she had a lover. This is crushing, even though the man obviously did not know this before he died.
  • We feel redemption in an artist who died in poverty but achieved posthumous fame.
• We tend to want to capture a moment (through a camera) rather than fully experiencing it—even if we never look at the video again.
• An experiencing self declares “I will never forget this moment”; the remembering self frequently forgets.

These examples challenge the idea that humans have consistent preferences and know how to maximize them (the rational agent model). We will consciously articulate that we prefer pain to be brief and pleasure to last, but our remembering self has different ideas.

(Shortform note: how might duration neglect and peak intensity be evolutionarily advantageous?

Maybe it makes us more resilient to painful episodes. If we strictly assessed utility by integrating the area under the curve, a very traumatic experience could leave us in “happiness debt” that would take considerable time to overcome.)

Seeming Exceptions

There are yet exceptions to the principles we’ve covered. If duration neglect is so strong, why does a painful labor that lasts 24 hours seem worse than one lasting 6 hours? Why does a 6 day vacation seem better than 3?

Kahneman argues that the mechanism of the longer duration is in changing the end state—a mother is more helpless after 24 hours than after 6; the vacationer is more relaxed after 6 days.

(Shortform note: another possible exception—if the remembering self makes the decisions tyrannically, why are good behaviors like flossing, losing weight, and saving money so difficult? The experiencing self endures short-term pain, but the remembering self should discount the pain and remember the benefits. Even better, the experiencing self in the future enjoys the fruits of labor of the past experiencing self!

It could be that the remembering self doesn’t actually experience the pleasure of long-term gains. Better health in your 30’s rewards you when you’re 70, which you’ve never experienced. Meanwhile, the memory of a delicious hamburger looms larger. The same goes with saving for retirement—if you’re younger, you have no memory of being financially secure in retirement, but you do remember how that last impulse purchase made you happy.)

Part 5-2: Experienced Well-Being vs Life Evaluations

Measuring Experienced Well-Being

How do you measure well-being? The traditional survey question reads: “All things considered, how satisfied are you with your life as a whole these days?”

Kahneman was suspicious that the remembering self would dominate the question, and that people were terrible at “considering all things.” The question tends to trigger the one thing that gives immense pleasurable (like dating a new person) or pain (like an argument with a co-worker).

To measure experienced well-being, he led a team to develop the Day Reconstruction Method, which prompts people to relive the day in detailed episodes, then to rate the feelings. Following the philosophy of happiness being the “area under the curve,” they conceived of the metric U-index: the percentage of time an individual spends in an unpleasant state.

They reported these findings:

• There was large inequality in the distribution of pain. 50% of people reported going through a day without an unpleasant episode. But a minority experience considerable emotional distress for much of the day, for instance from illness, misfortune, or personal disposition.
• Different activities have different U-indices. Morning commute: 29%; childcare: 24%; TV watching: 12%; sex: 5%.
• The weekend’s U-index is 6% lower than weekdays, possibly because people have more control over putting time into pleasurable activities.
• Different cultures show different U-indices for the same activities. Compared to American women, French women spend less time with children but enjoy it more, perhaps because of more access to child care. French women also spend the same amount of time eating, but they enjoy it more, possibly because they mentally focus on it rather than mindlessly eat in a rush.
• Your current mood depends largely on the current situation, not on general factors influencing general satisfaction.
  • Things that affect mood: coworker relations, loud noise, time pressure, a boss hovering around you.
  • Things that do not affect mood: benefits, status, pay.
• Some activities generally seen as positive (like having a romantic partner) don’t improve experienced well-being. This might be partially because of tradeoffs—women in relationships spend less time alone, but they also have less time with friends. They spend more time having sex, but they also spend more time doing housework and caring for children.

Suggestions for Improving Experienced Well-being

How can you improve your moment-to-moment happiness?

• Focus your time on what you enjoy. Commute less.
• To get pleasure from an activity, you must notice that you’re doing it. Avoid passive leisure time in places like TV, and spend more time in active leisure time, like socializing and exercise.

Reducing the U-index should be seen as a worthwhile societal goal. Reducing the U-index by 1% across society would be a huge achievement, with millions of hours of avoided suffering.

Experienced Well-Being vs Life Evaluations

Where well-being is measured by methods like the Day Reconstruction Method, life evaluation (or life satisfaction) is measured by the Cantril Self-Anchoring Striving Scale:

“Please imagine a ladder with steps numbered from zero at the bottom to 10 at the top. The top of the ladder represents the best possible life for you and the bottom of the ladder represents the worst possible life for you. On which step of the ladder would you say you personally feel you stand at this time?”

Compared to the moment-by-moment experience of well-being, this question takes a broader view of where you are in life.

Some things affect experience and life evaluation differently:

• Things that affect life evaluation more than experience
  • Education
  • Money: in the United States, after about $75,000 of annual income, more money increases evaluation without increasing experience.
    • One theory to explain this: a higher income might reduce ability to enjoy small pleasures of life. A simple bar of chocolate might be more enjoyable when you have less wealth.
• Things that affect experience more than life evaluation
  • Ill health
  • Living with children
  • Religion

Temperament, which is largely determined by genetics, affects both experienced well-being and life satisfaction.

• This can explain why certain changes like marriage show low correlations with well-being - it works for some and not for others.

Goals make a big difference in satisfaction.

• People who care about money and get it are more satisfied than those who wanted money and didn’t get it, or those who didn’t care about money and didn’t get it.
• One recipe for dissatisfaction: setting goals that are especially difficult to attain. (The goal that led to the most dissatisfaction: “becoming accomplished in a performing art.”)

Severe poverty amplifies the experienced effects of misfortunes.

• For the top ⅔ of individuals by wealth, a headache increases negative experience from 19% to 38%. For the poorest tenth, it starts at 38% and moves to 70%. Not only do the poor have a higher setpoint of negative experience, a misfortune increases the negative experience. The same result applies to divorce and loneliness.
• The beneficial effects of the weekend are smaller for the poor.

Focusing Illusion

Considering overall life satisfaction is a difficult System 2 question. When considering life satisfaction, it’s difficult to consider all the factors in your life, weigh those factors accurately, then score your factors.

As is typical, System 1 substitutes the answer to an easier question, such as “what is my mood right now?”, focusing on significant events (both achievements and failures), or recurrent concerns (like illness).

The key point: Nothing in life is as important as you think it is when you are thinking about it. Your mood is largely determined by what you attend to. You get pleasure/displeasure from something when you think about it.

For example, even though Northerners despise their weather and Californians enjoy theirs, in research studies, climate makes no difference in life satisfaction.

Why is this? When people are asked about life satisfaction, climate is just a small factor in the overall question. You tend to think much more about your love life, your career, your family and friends, and the bills you need to pay. Climate is likely a distant concern.

However, when you consider the question, “are Californians more satisfied with life than Northerners because of the weather,” climate becomes a focal point. You overweight the climate factor in the life satisfaction question; you conjure the available image of hiking, rather than the reality that lives are similar throughout; you overestimate how often Californians think about the weather when asked about a global evaluation.

This idea leads to a number of counter-intuitive results:

• Consider the question: “how much pleasure do you get from your car?” Now a different question: “when do you get pleasure from your car?”
  • The answer to the second question is when you think about it—which is not often, including when you’re driving it.
  • However, to answer the broader first question, you substituted the easier, narrower question: “how much pleasure do you get from your car when you do think about it?”
• Chronic stressors cause more dissatisfaction than you would predict. This includes chronic pain, chronic loud noise, and depression. By being ever-present, these stressors constantly bring the problem into central focus.
• Certain activities that engage you—like social activities—retain your focus and give you more.

Mispredictions of Happiness

The focusing illusion leads to mispredictions of happiness, for ourselves and others.

When you forecast your own future happiness, you overestimate the effect a change will have on you (like getting a promotion), because you overestimate how salient the thought will be in future you’s mind. In reality, future you has gotten used to the new environment and now has other problems to worry about.

You may pay significant amounts for improvements in life satisfaction, even though it has no effect on experienced happiness.

• Colostomy patients show no difference in experienced happiness compared to healthy people. Yet they would trade away years of life for no longer having a colostomy.
• The remembering self has a focusing illusion about life that the experiencing self endures comfortably.

However, when you predict the happiness of others, you focus on the aspects of their experience that are most salient to you. You ignore that the person may have habituated to her circumstances, or that the aspect has counterbalancing benefits or drawbacks.

• If you’re preoccupied with lacking money, you predict wealthier people are happier than they are, even though they’ve adjusted to wealth and are likely no happier than you are.
• People predict paraplegics have a higher U-index than they really do. After adjustment, paraplegics stop thinking about their condition. They enjoy friends and get mad about politics, just like you.

Adaptation to a new situation consists in large part of thinking less and less about it.

Antidotes to the Focusing Illusion

(Shortform note: the following are our additions and not explicitly described in the book.)

• To evaluate your life satisfaction, create a life rubric, where you list the factors and their weightings, then score each of the factors. This might make you happier and grateful for what you have, rather than focusing on single sore points that stick out.
• Choose to spend time on pleasurable activities that will engage your focus. You pay little attention to the TV as you passively watch, but you retain focus in social interaction or playing team sports.
• Reflect on your past experiences to inform future ones—how much did buying something in the past make you happier today? What activity are you really thankful to your past self for doing? Do more of what you appreciate your past self for having done.

Conclusions on Happiness

Putting it all together - which self should we cater to, the remembering self or the experiencing self?

In Thinking, Fast and Slow, Kahneman doesn’t have a clear answer, but he rules out that either the remembering self or the experiencing self should be focused on exclusively.

Catering only to the remembering self invites unnecessary suffering. Our memories are fallible, being subject to duration neglect and peak-end rule.

• The remembering self favors short periods of intense joy over long periods of moderate happiness.
• The remembering self avoids long happy periods if it knows a poor ending will come.
• In the extreme, the remembering self would endure decades of pain ending in one jubilee right before death, remembering that joyful moment in the last minutes of life.

Catering only to the experiencing self treats all moments of like alike, regardless of the future benefit.

• Some instances have memories that give more value than others.
• A moment can also alter the experience of subsequent moments.
  • Learning music can enhance future playing or listening for years.
  • A traumatic event can cause PTSD and misery over a lifetime.
  • Making money today can unlock new experiences for your future experiencing self.
• In the extreme, the experiencing self would greedily pursue whatever maximized happiness this moment, with little regard for the future self.

Both the remembering self and the experiencing self must be considered—their interests do not always coincide.

For a population, it’s not clear which to maximize, say for treating health conditions. Should we minimize experienced pain, or should we solve whatever people are most willing to pay to be relieved from? These are all fruitful questions for continuing research and philosophy.

Shortform Exclusive: Checklist of Antidotes

As an easy reference, here’s a checklist of antidotes covering every major bias and heuristic from the book.

Cognitive Biases and Heuristics

• To block System 1 errors, recognize the signs that you’re in trouble and ask System 2 for reinforcement.
• Observing errors in others is easier than in yourself. So ask others for review. In this way, organizations can be better than individuals at decision-making.
• To better regulate your behavior, make critical choices in times of low duress so that System 2 is not taxed.
  • Order food in the morning, not when you’re tired after work or struggling to meet a deadline.
  • Notice when you’re likely to be in times of high duress, and put off big decisions to later. Don’t make big decisions when nervous about others watching.
• In general, when estimating probability, begin with the baseline probability. Then adjust from this rate based on new data. Do NOT start with your independent guess of probability, since you ignore the data you don’t have.
• WYSIATI
  • Force yourself to ask: “what evidence am I missing? What evidence would make me change my mind?”
• Ordering effect
  • Before having a public discussion on a topic, elicit opinions from the group confidentially first. This avoids people from getting their first biased by the first speakers.
• Reversion to the mean
  • Question whether high performers today are merely outliers who will revert to the mean.
  • When looking at high and low performers, question what fundamental factors are actually correlated with performance. Then, based on these factors, predict which performers will continue and which will revert to the mean.
• Anchors
  • In negotiations, when someone offers an outrageous anchor, don’t engage with an equally outrageous counteroffer. Instead, threaten to end the negotiation if that number is still on the table.
  • If you’re given one extreme number to adjust from, repeat your reasoning with an extreme value from the other direction. Adjust from there, then average your final two results.
• Availability bias
  • Force yourself to lower the weight on more available things. Especially be wary of things you see repeated often in news or advertising, and of things that strongly trigger extreme emotions.
  • Be aware of “common sense” intuitions that seem true merely because it’s repeated often, like “searing meat seals in the juices.”
• Representativeness
  • To avoid the “Tom W. librarian” problem, use Bayesian statistics. Start by predicting the base rates, using whatever factual data you have. Then consider how the new data should influence the base rates.
• Conjunction fallacy
  • When hearing a complicated explanation that has too many convenient assumptions or vivid details (like an investment pitch for a business or an explanation for what caused a phenomenon), be aware that each additional assumption lowers the likelihood of it being true.
• Hindsight/Outcome Bias
  • Keep a journal of your current beliefs and what you estimate the outcomes to be. In the future, once the outcomes are known, reflect on your beliefs at the time to see how accurate you were.
  • Reward people based on the decisions they make at the time with the information they had, before the outcomes come out. Don’t reward people who took outlandish risks but got lucky.
• Using algorithms over intuition
  • Standardize the hiring interview. Make a list of traits important for success in the role. Then create direct questions to assess the trait, and a rubric. Score each person on all traits in the rubric. Finally, hire the person with the highest score, period.
  • This can be generalized to any decision process.
• Planning fallacy
  • Write a premortem. “Imagine that it’s a year from now. We implemented the plan. It was a disaster. Write a history of the disaster.”
• Invert the question.
  • How can this project fail?
  • Turn a loss into a gain and re-ask the question, and vice versa.
• Use formulas and checklists to avoid biases.
• Use biases to your advantage by overcoming your fears and problems
  • When feeling a negative emotion, surround yourself with available info on the inverse positive emotion (for example, on ways you feel competent or a vision of your project’s success).
  • Improve your mood by considering negative outcomes as costs rather than losses. For example, a failed project is the cost of learning the lesson, rather than a dead loss.

Prospect Theory

• Be aware of how much you value probabilities in the extremes. 1% appears far better than 0%, and 100% appears far better than 99%.
• Framing effects
  • Invert the framing to a complementary view. Turn an increase in mortality into a decrease in survivability, and vice versa.
• Endowment effect
  • Be wary of when you prize the status quo merely because it’s the status quo.
• Denominator neglect
  • Reduce all decisions down to a single fungible metric, in the broadest account possible, to allow global calibration. For example, benefits to human life can be assessed in terms of Quality Adjusted Life Years per $, so that repairing glaucoma can be compared to childhood cancers.
• Narrow framing
  • Adopt risk policies: simple rules to follow in individual situations that give a better broad outcome.
  • Deliberately consider the broad range of alternatives for scarce resources—time, labor, money. Be aggressive with defining the global set of opportunity costs.

Happiness

• Improving experienced happiness
  • Focus your time on what you enjoy. Commute less.
  • To get pleasure from an activity, you must notice that you’re doing it. Avoid passive leisure time in places like TV, and spend more time in active leisure time, like socializing and exercise.
• Focusing illusion
  • To evaluate your life satisfaction, create a life rubric, where you list the factors and their weightings, then score each of the factors. This might make you happier and grateful for what you have, rather than focusing on single sore points that stick out.
  • Reflect on your past experiences to inform future ones—how much did buying something in the past make you happier today? What activity are you really thankful to your past self for doing? Do more of what you appreciate your past self for having done.
• Cater to both your remembering self and your experiencing self.